Columbia University, via Coursera

Natural Language Processing notes by Asim Ihsan is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
There are excellent readings assigned to the class. They’re explicitly inlined into the respective lecture, to save typing stuff out twice.
Other readings (papers, textbooks, other courses) are explicitly inlined as well.
In order to use pandoc run (need to include custom LaTeX packages for some symbols):
pandoc \[course\]\ natural\ language\ processing.md
-o pdf/nlp.pdf --include-in-header=latex.template
or, for Markdown + LaTex to HTML + MathJax output:
pandoc \[course\]\ natural\ language\ processing.md
-o html/nlp.html
--include-in-header=html/_header.html
--mathjax -s --toc --smart -c _pandoc.css
and, for the ultimate experience, after pip install watchdog:
watchmedo shell-command --patterns="*.md"
--ignore-directories --recursive
--command='<command above>' .
- What is NLP?
- Computers using natural language as input and/or output.
- NLU: understanding, input
- NLG: generation, output.
Tasks
- Oldest task: machine translation. Convert between two languages.
- Information extraction
- Text as input, structure of key content as output.
- e.g. job posting into industry, position, location, company, salary.
- Complex searches (“jobs in Boston paying XXX”).
- Statistical queries (“how has jobs changed in IT changed over time?”)
- Text summarization
- Dialogue systems
- Humans can interact with a computer to ask questions and achieve tasks.
Basic NLP problems
- Tagging
- Map strings to tagged sequences (each word is lexed and tagged with an appropriate label).
- Part-of-speech tagging: noun, verb, preposition, …
- Profits (N) soared (V) at (P) Boeing (N)
- Named Entity Recognition: companies, locations, people
- Profits (NA) soared (NA) at (NA) Boeing (C)
- Parsing
- e.g. “Boeing is located in Seattle” into a parse tree.
Why is NLP hard?
- Ambiguity
- “At last, a computer that understands you like your mother”; three intrepretations at the syntactic level.
- But also occurs at an acoustic level: “like your” sounds like “lie cured”.
- One is more likely than the other, but without this information difficult to tell.
- At semantic level, words often have more than one meaning. Need context to disambiguate.
- “I saw her duck with a telescope”.
- At discourse (multi-clause) level.
- “Alice says they’ve built a computer that understands you like your mother”
- If you start a sentence saying “but she…”, who is she referring to?
What will this course be about
- NLP subproblems: tagging, parsing, disambiguation.
- Machine learning techniques: probabilistic CFGs, HMMs, EM algorithm, log-linear models.
- Applications: information extraction, machine translation, natural language interfaces.
- Language modelling, smoothed estimation
- Tagging, hidden Markov models
- Statistical parsing
- Machine translation
- Log-linear models, discriminative methods
- Semi-supervised and unsupervised learning for NLP
- We have some finite vocabulary, i.e.
\[V = \{the, a, man telescope, Beckham, two, ...\}\]
- We have countably infinite set of strings, which are the set of possible sentences in the language:
\[V^+ = \{"the\:STOP", "a\:STOP", "the\:fan\:STOP", ...\}\]
- STOP is a stop symbol at the end of a sentence. Convenient later on.
- Sentences don’t have to make sense, just every sequence of words.
Also a sentence could just be {“STOP”}, empty.
- We have a training sample of example sentences in English.
- Sentences from the New York Times in the last 10 years.
- Sentences from a large set of web pages.
- In the 1990’s 20 million words common, by the end of the 90’s 1 billion words common.
- Nowadays 100’s of billions of words.
With this training sample we want to “learn” a probabiliy distribution p, i.e. p is a function that satisfies:
\[\sum_{x \in V^+} p(x) = 1, \quad p(x) \ge 0 \; \forall \; x \in V^+\]
- For any sentence x in language, p(x) >= 0.
- If we sum over all sentences x in language, p(x) sums to 1.
- A good language model assigns high probabilities to likely sentences in English (the fan saw Beckham STOP), low probabilities to unlikely sentences in English (Beckham fan saw the STOP)
- But…why do we want to do this?!
- Speech recognition was original motivation; related problems are optical character recognition and handwriting recognition.
- Input: sound wave time series.
- Preprocess: split into relatively short time periods, e.g. 10ms.
- For each frame do a Fourier transform, get energies of frequencies.
- Problem is to output recognised speech, sequence of words.
- Main course notes: it’s useful to have prior probabilities so that if we can choose between alternatives we can ask “which is most likely?”.
- “recognise speech” vs “wreck a nice beach”
- The estimation techniques developed for this problem will be very useful for other problems in NLP.
- Naive method of language modelling
- We have N training sentences.
- For any sentence \(x_1, ..., x_n\), define \(c(x_1, ..., x_n)\) as the number of times the sentences is seen in our training data.
- Naive estimate:
\[p(x_1, \ldots, x_n) = \frac{c(x_1, \ldots, x_n)}{N}\]
- This is a valid, well-formed language model (p(x) sums to 1, they’re all >= 0).
- However, they’ll assign a probabiliy of 0 to any unseen sentences; no ability to generalise to new sentences.
- How can we build language models that generalise beyond the test sentences?
- Markov Processes
- Consider a sequence of random variables \(X_1, X_2, \ldots, X_n\).
- Each random variable can take any value in a finite set V.
- For now assume n is fixed, e.g. = 100. Every sequence is the same length.
- Our goal: model the joint probability distribution of the values of these n variables:
\[P(X_1 = x_1, X_2 = x_2, \ldots, X_n = x_n)\]
This is huge: for vocabulary V, number of sequences of length n is \(|V|^n\).
- First-Order Markov Processes
- Going to use the chain rule of probabilities to decompose the expression into a product of expressions.
For two expressions, this rule is:
\[P(A,B) = P(A) \times P(B|A)\] \[P(A,B,C) = P(A) \times P(B|A) \times P(C|A,B)\]
\[P(X_1 = x_1, X_2 = x_2) = P(X_1 = x_1) \times P(X_2 = x_2 | X_1 = x_1)\] \[P(X_1 = x_1, X_2 = x_2, X_3 = x_3) = ... P(X_3 = x_3 | P(X_2 = x_2, X_1 = x_1)\]
- This kind of decomposition is exact: this is always true, and no assumptions are involved.
- Hence the general decomposition:
\[P(X_1 = x_1, X_2 = x_2, \ldots, X_n = x_n)\] \[=P(X_1 = x_1) \prod_{i=2}^{n} P(X_i = x_i\;|\;X_1 = x_1, \dots, X_{i-1} = x_{i-1})\]
- Continuing on, with first-order Markov assumption:
\[= P(X_1 = x_1) \prod_{i=2}^{n} P(X_i = x_i\;|\; X_{i-1} = x_{i-1})\]
- The first-order Markov assumption: for any \(i \in \{2, \dots, n\}\), for any \(x_1, \dots, x_n\):
\[P(X_i=x_i|X_1=x_1, \ldots, X_{i-1} = x_{i-1}) = P(X_i=x_i | X_{i-1} = x_{i-1})\]
- Random variable at position i depends on just the previous value, on the variable at position (i-1).
- \(X_i\) is conditionally independent of all the other random variables once you condition on \(X_{i-1}\).
- What about Second-Order Markov Processes?
- Again, the problem is to model the joint distribution over \(n\) random variables:
\[P(X_1 = x_1, X_2 = x_2, \ldots, X_n = x_n)\] \[=P(X_1 = x_1) P(X_2 = x_2 | X_1 = x_1) \prod_{i=3}^{n} P(X_i = x_i | X_{i-2} = x_{i-2}, X_{i-1} = x_{i-1})\]
- For elements further along in the sequence the value for the i’th random variable depends on the previous two random variables.
- This is a bit awkward, so for convenience we assume \(x_0 = x_{-1} = *\), where \(*\) is a special “start” symbol.
\[= \prod_{i=1}^{n} P(X_i = x_i | X_{i-2} = x_{i-2}, X_{i-1} = x_{i-1})\]
- For example, \(x_{-1} = *,\;x_0 = *,\;x_1 = the,\;\ldots\),
- Want \(n\) to also be a random variable.
- Simple solution: always define \(X_n = STOP\), where \(STOP\) is a special symbol.
- Use a Markov process as before, but assume \(X_n = STOP\).
- A trigram language model consists of:
- A finite set \(V\) (the words, the vocabulary).
- A parameter \(q(w|u,v)\) for each trigram \(u,v,w\) such that \(w \in V \bigcup \{STOP\}\), and \(u,v \in V \bigcup \{*\}\).
- For each trigram \(u,v,w\), a sequence of three words, we have a parameter \(q(w|u,v)\).
- \(w\) could be any element of V or STOP, and
- \(u,v\) could be any element of V or START.
- For any sentence \(x_1, \ldots, x_n\) where \(x_i \in V\) for \(i = 1 \ldots (n-1)\), and \(x_n = STOP\), the probability of the sentence under the trigram model is:
\[p(x_1, \dots, x_n) = \prod_{i=1}^{n}q(x_i\;|\;x_{i-2},x_{i-1})\]
- where we define \(x_0 = x_{-1} = *\).
- i.e. for any sentence the probability of it is the product of second-order Markov probabilities of its constituent trigrams.
An example. For the sentence
the dog barks STOP
we could have
\(p(\textrm{the dog barks STOP}) =\)
\(q(\textrm{the | *, *})\)
\(\times q(\textrm{dog | *, the})\)
\(\times q(\textrm{barks | the, dog})\)
\(\times q(\textrm{STOP | dog, barks})\)
- This is still a naive language model. It’s easy to find problems.
- PCFGs, explored later, are much superior.
- Having said that, trigram language models are extremely useful.
- They are very hard to improve upon.
- Considerable simplicity.
- Quiz: say we have a language model with \(V = \{\textrm{the, dog, runs}\}\), and the following parameters:
\[
\begin{align}
&\begin{aligned}
q(\textrm{the | *, *}) & = 1 \\
q(\textrm{dog | *, the}) & = 0.5 \\
q(\textrm{STOP | *, the}) & = 0.5 \\
q(\textrm{runs | the, dog}) & = 0.5 \\
q(\textrm{STOP | the, dog}) & = 0.5 \\
q(\textrm{STOP | dog, runs}) & = 1
\end{aligned}
\end{align}
\]
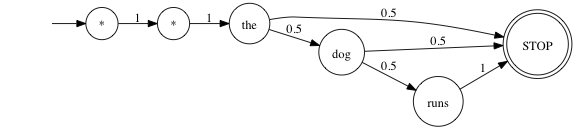
- There are three sentences with non-zero probability under this model.
- {*, *, the, STOP}
- {*, *, the, dog, STOP}
- {*, *, the, dog, runs, STOP}
- Draw out a graph, where nodes are words and edge labels denote probabilities, to see this:
- The above is a Markov chain drawn in the style of a finite-state machine. This is a lot of fancy talk for a very simple idea.
- People call these sorts of diagrams all sorts of fancy names.
- Mathematicians call this type of diagram a graph. (No, not a pie chart).
- Since there are arrows in this diagram this is a directed graph.
- If the digram just had plain lines, without arrow heads, it would be an undirected graph.
- Computer scientists call this type of diagram a finite-state machine (FSM).
- Electrical engineers call diagrams that (kind of) look like this Markov chains.
- In graph-speak, each circle is a node and each arrow is an edge.
- In FSM-speak, each circle is a state and each arrow is a transition.
- People will often use node/state and edge/transition interchangably, and others love pointing out that they’re using the wrong words.
- Every circle and double circle represents a state. A state is “somewhere you can be”, which’ll make sense soon.
- Every line is the likelihood of moving from one state to another. If this number is 0 this transition is impossible, if it is 1 it is certain, and could be something in between.
- This number can never be less than 0 or greater than 1. If it is then the probability distribution is no longer “well-formed”, i.e. doesn’t make sense.
- On the left-hand side an arrow appears to come out of nowhere to the first start symbol (*). This is the start state.
- Every double circle is an accepting state. The only accepting state is the STOP symbol.
- Take your finger and trace out every path from every start state to every accepting state. This is a possible sequence of words in this language model.
- As the STOP symbol is the only accepting state, every sequence of words in this language model must end with the STOP symbol.
- The probability of a given sequence of words is the product of all the edge probabilities.
- The sum of probabilities of all possible sequences of words must add up to one if the language model is “well-formed”.
- One of the rules of a probability distributions is that all the “little probabilities”, or probabilities of individual events, must sum to 1 or else it just doesn’t make sense.
- You’ll notice something peculiar. If any edge has a value of 0 then all sequences of words that include that edge must be impossible, no matter how likely the other transitions in that sequence!
- Hence when you’re tracing your finger looking for possible sequences you exclude any paths that include an edge with a probability of 0.
- You may be wondering how hard this gets with many nodes and many edges. Very hard. This is just a visual depiction of how utterly impossible brute force is when it comes to language models, and hence how important the upcoming Vitterbi algorithm is.
- But what are the values of parameters q?
- This turns out to be a challenging problem.
- A natural estimate: the maximum likelihood estimate (ML).
- Recall that we assume that we have a training set, some example sentences in our language, typically, as you recall, millions or billions of sentences.
- From these sentences we can derive counts; how often do trigrams occur?
\[q(w_i\;|\;w_{i-2},w_{i-1}) = \frac{\textrm{Count}(w_{i-2},w_{i-1},w_{i})}{\textrm{Count}(w_{i-2},w_{i-1})}\]
\[q(\textrm{laughs | the, dog}) = \frac{\textrm{Count(the, dog, laughs)}}{\textrm{Count(the, dog)}}\]
- This is intuitive. For instances of a particular bigram how often are they followed by the particular third word of our trigram?
- Quiz: consider the following corpus of sentences:
- the dog walks STOP
- walks the dog STOP
- dog walks fast STOP
- Let \(q_{ML}\) by the maximum-likelihood parameters of a trigram langauge model trained on this corpus. Which of the following parameters have a value that is both well-defined and non-zero?
Correct:
\(q_{ML}({\textrm{walks | *, dog}})\)
\(q_{ML}({\textrm{dog | walks, the}})\)
\(q_{ML}({\textrm{walks | the, dog}})\)
Incorrect:
\(q_{ML}({\textrm{walks | dog, the}})\)
\(q_{ML}({\textrm{fast | dog, the}})\)
\(q_{ML}({\textrm{STOP | walks, dog}})\)
- ML is a useful starting point, but has serious problems.
Spare Data problems
- Say our vocabulary size is \(N = |V|\), then there are \(N^3\) parameters in our model.
- e.g. \(N = 20,000\;\implies\;20,000^3 = 8 \times 10^{12}\) parameters.
- Most parameters will be zero; most possible trigrams will not appear.
- But does that mean all trigrams we haven’t seen are necessarily impossible to ever see? No.
- Worse still, the bigram denominator may be zero, and the ML ratio is undefined.
- We have some test data, \(m\) sentences, i.e. \(s_1, s_2, s_3, \ldots, s_m\). Each of these is a sentence in the language, e.g. {the dog laughs STOP}.
- Additionally, assume that use some development data to determine the language model parameters, but hold out some additional test data to evaluate the language model.
- Natural to look at the probability that our language model gives to sentences in the test data \(\prod_{i=1}^{m}p(s_i)\); it’s never seen it before.
\[\textrm{log}\;\prod_{i=1}^{m} p(s_i) = \sum_{i=1}^{m} \textrm{log}\;p(s_i)\]
- (the above is a basic rule of logarithms; log of product = sum of logs).
- recall that e.g.:
\[p(s_i) = q(\textrm{the | *, *}) \times q(\textrm{dog | *, the}) \times \ldots\]
- Naturally we’d expect better languages models to assign higher probabilities to sentences in the test data.
And log is a monotonically increasing function, so expect the sum of logs to correspondingly be higher for better language models.
In fact, the usual evaluation measure is perplexity:
\[\textrm{Perplexity} = 2^{-l},\;\textrm{where}\] \[l = \frac{1}{M} \sum_{i=1}^{m} \textrm{log}\;p(s_i)\]
- and M is the total number of words in the test data. In some sense with (1/M) the perplexity is now stable with respect to the size of the test data.
- The lower the perplexity the better the fit of the language model to the test data.
Some Intuition about Perplexity
- Say we have vocabulary \(V\), and \(N = |V| + 1\), and the dumbest possible model predicts:
\[q(w|u,v) = \frac{1}{N},\;\forall\;w \in V \cup \{\textrm{STOP}\},\;\forall\;u,v \in V \cup \{\textrm{*}\}\].
- This dumbest model assigns the uniform distribution over all possible words in each possible. Ignores previous words, doesn’t measure relative frequency.
- Easy to calculate perplexity:
\[\textrm{Perplexity} = 2^{-l},\;\textrm{where}\;l=\textrm{log}\;\frac{1}{N}\] \[\implies\; \textrm{Perplexity} = N\]
- !!AI implying all these calculations use log base 2.
- Perplexity is a measure of effective “branching factor”.
- The model is as confused on test data as if it had to choose uniformly and independently among P possibilities per word, where P is the perplexity. Source: Wikipedia:Perplexity.
Quiz: define a trigram language model with the following parameters:
- q(the | *, *) = 1
- q(dog | *, the) = 0.5
- q(cat | *, the) = 0.5
- q(walks | the, cat) = 1
- q(STOP | cat, walks) = 1
- q(runs | the, dog) = 1
- q(STOP | dog, runs) = 1
Now consider a test corpus with the following sentences:
- the dog runs STOP
- the cat walks STOP
- the dog runs STOP
Note that the number of words in this corpus, M, is 12.
What is the perplexity of the language model, to 3dp?
\[P = 2^{-l}\] \[l = \frac{1}{M} \sum \textrm{log}_2\{p(s_i)\}\]
\(p(\textrm{the dog runs STOP}) = q(\textrm{the | *, *}) \times q(\textrm{dog | *, the}) \times q(\textrm{runs | the, dog}) \times q(\textrm{STOP | dog, runs})\)
\(= 1 \times 0.5 \times 1 \times 1 = 0.5\)
\(p(\textrm{the cat walks STOP}) = q(\textrm{the | *, *}) \times q(\textrm{cat | *, the}) \times q(\textrm{walks | the, cat}) \times q(\textrm{STOP | cat walks})\)
\(= 1 \times 0.5 \times 1 \times 1 = 0.5\)
\(l = \frac{1}{12} \{ 3 \times \textrm{log}_2(0.5) \}\) \(=\frac{1}{12}(-3) = \frac{-1}{4}\)
\(p=2^{\frac{1}{4}} = \sqrt[4]{2} = 1.189\;\textrm{(3dp)}\)
- \(|V| = 50,000\).
- Trigram model, second-order Markov process, \(p(x_1 \dots x_n) = \prod_{i=1}^{n} q(x_i|x_{i-2},x_{i-1})\) gave perplexity = 74.
- This is vastly smaller than the vocabulary size, so this is vastly superior to the uniform distribution.
- Bigram model, a first-order Markov process, \(p(x_1 \ldots x_n) = \prod_{i=1}^{n}q(x_i|x_{i-1})\) gave perplexity = 137.
- Unigram model, \(p(x_1 \ldots x_n) = \prod_{i=1}^{n} q(x_i)\), gave perplexity = 955.
- Predicting each word without using context of previous words.
- Shannon conducted experiments on entropy of English. See “Prediction and entropy of printed English”, 1951.
- Chomsky, in “Syntactic Structures”, 1957
- “Colorless green ideas sleep furiously”
- “Furiously sleep ideas green colorless”
- Argues probability has little to offer for semantic sense and grammatical validity.
- Very much against Shannon’s experiments with Markov processes and language.
- Later in the course we’ll look at PCFGs that capture long-range dependencies.
- Recall the “Sparse Data Problems” section before.
\[q_{ML}(w_i\;|\;w_{i-2},w_{i-1}) = \frac{\textrm{Count}(w_{i-2},w_{i-1},w_i)}{\textrm{Count}(w_{i-2},w_{i-1})}\]
\[q_{ML}(w_i\;|\;w_{i-1}) = \frac{\textrm{Count}(w_{i-1},w_i)}{\textrm{Count}(w_{i-1})}\]
\[q_{ML} = \frac{\textrm{Count}(w_i)}{\textrm{Count}()}\]
- The trigram MLE’s advantage is that it conditions on a lot of context, so given sufficient training data these counts will be high and it will converge to the “true value”.
- This has relatively low bias. It is able to generalise from one particular training set to other unknown data.
- The unigram MLE completely ignores context, and so it will converge to a less-good estimator as the number of training samples increases.
- This has relatively high bias.
- The trigram MLE’s disadvantage is that many counts will be equal to zero, so we need many samples to get a good estimate.
- This has relatively high variance. It needs far more data to be able to generalise; if it has insufficient data it will not learn / generalise.
- The unigram MLE’s count will converge relatively quickly to their expected value, and so don’t need many samples.
- The bigram MLE is in between the trigram MLE and unigram MLE.
- Take our estimate \(q(w_i\;|\;w_{i-2},w_{i-1})\) to be:
\(= \lambda_1 \times q_{ML}(w_i\;|\;w_{i-2},w_{i-1})\)
\(+ \lambda_2 \times q_{ML}(w_i\;|\;w_{i-1})\)
\(+ \lambda_3 \times q_{ML}(w_i)\)
- where \(\lambda_1 + \lambda_2 + \lambda_3 = 1\) and \(\lambda_i \ge 0\;\forall\; i\).
- New estimate is a weighted average of the three MLEs.
- For example, assuming \(\lambda_1 = \lambda_2 = \lambda_3 = \frac{1}{3}\)
\(q(\textrm{laughs | the, dog})\)
\(= \frac{1}{3} \times q_{ML}(\textrm{laughs | the, dog})\)
\(+ \frac{1}{3} \times q_{ML}(\textrm{laughs | dog})\)
\(+ \frac{1}{3} \times q_{ML}(\textrm{laughs})\)
Quiz: we are given the following corpus:
- the green book STOP
- my blue book STOP
- his green house STOP
- book STOP
Assume we compute a language model based on this corpus using linear interpolation with \(\lambda_i = \frac{1}{3}\;\forall\;i \in \{1,2,3\}\).
What is the value of the parameter \(q_{LI}(\textrm{book | the, green})\) in this model to 3dp? (Note: please include STOP words in your unigram model).
\(q_{LI}(\textrm{book | the, green})\)
\(= \frac{1}{3} \times q_{ML}(\textrm{book | the, green})\)
\(+ \frac{1}{3} \times q_{ML}(\textrm{book | green})\)
\(+ \frac{1}{3} \times q_{ML}(\textrm{book})\)
\(= \frac{1}{3} \times \frac{\textrm{Count(the, green, book)}}{\textrm{Count(the, green)}}\)
\(+ \frac{1}{3} \times \frac{\textrm{Count(green, book)}}{\textrm{Count(green)}}\)
\(+ \frac{1}{3} \times \frac{\textrm{Count(book)}}{\textrm{Count()}}\)
\(= \frac{ \frac{1}{3}(1) }{(1)} + \frac{ \frac{1}{3}(1) }{(2)} + \frac{ \frac{1}{3}(3) }{(14)}\)
\(= 0.571\;\textrm(3dp)\)
Our estimate correctly defines a distribution. Define \(V^{'} = V \cup \{STOP\}.\)
\(\sum_{w \in V^{'}} q(w|u,v)\)
\(=\sum_{w \in V^{'}} [\lambda_1 \times q_{ML}(w|u,v) + \lambda_2 \times q_{ML}(w|v) + \lambda_3 \times q_{ML}(w)]\)
move out the constant lambdas:
\(=\lambda_1 \sum_w q_{ML}(w|u,v) + \lambda_2 \sum_w q_{ML}(w|v) + \lambda_3 \sum_w q_{ML}(w)\)
By definition the maximum likelihood estimates in a given trigram, bigram, or unigram model sum to 1. Intuitively, the probability of each given trigram, bigram, or unigram probability in the model sums to 1.
\(= \lambda_1 + \lambda_2 + \lambda_3 = 1\)
(Can also show that \(q(w|u,v) \ge 0\;\forall\;w \in V^{'}\)).
Quiz: say we have \(\lambda_1 = -0.5, \lambda_2 = 0.5, \lambda_3 = 1.0\). Note that these satisfy the constraint \(\sum_i \lambda_i = 1\), but violate the constraint that \(\lambda_i \ge 0\).
(Credit to Philip M. Hession for the explanations).
Recalling our definition of \(q\) above within: \(\sum_{w \in V^{'}} q(w|u,v)\), it’s hence true that there might be a trigram \(u,v,w\) such that \(q(w|u,v) \lt 0\):
\[q(\text{barks}|\text{the,dog})=-\frac{1}{2}\frac{c(\text{the,dog,barks})}{c(\text{the,dog})}+\frac{1}{2}\frac{c(\text{dog,barks})}{c(\text{dog})}+1\cdot\frac{c(\text{barks})}{c()}\]
- if \(c() \gg c(\text{barks})\)
- and if \(c(\text{dog}) \gg c(\text{dog,barks})\)
- and if \(c(\text{the,dog}) \approx c(\text{the,dog,barks})\)
then \(q(\text{barks}|\text{the,dog})=-\frac{1}{2}(\sim 1)+\frac{1}{2}(\ll 1)+1(\ll 1) \lt0\)
and there might be a trigram \(u,v,w\) such that \(q(w|u,v) \gt 1\):
\[q(\text{barks}|\text{the,dog})=-\frac{1}{2}\frac{c(\text{the,dog,barks})}{c(\text{the,dog})}+\frac{1}{2}\frac{c(\text{dog,barks})}{c(\text{dog})}+1\cdot\frac{c(\text{barks})}{c()}\]
- if \(c() \approx c(\text{barks})\)
- and if \(c(\text{dog}) \approx c(\text{dog,barks})\)
- and if \(c(\text{the,dog}) \gg c(\text{the,dog,barks})\)
then \[q(\text{barks}|\text{the,dog})=-\frac{1}{2}(\ll 1)+\frac{1}{2}(\sim 1)+1(\sim 1) \gt 1\]
It is not true that we may have a bigram \(u,v\) such that \(\sum_{w \in V} q(w|u,v) \neq 1\):
\[\sum_{w}q(w|u,v) = -\frac{1}{2}\frac{\sum_w c(u,v,w)}{c(u,v)}+\frac{1}{2}\frac{\sum_w c(v,w)}{c(v)}+1\cdot\frac{\sum_w c(w)}{c()} = -\frac{1}{2}(1)+\frac{1}{2}(1)+1(1)=1\]
since \(\sum_w c(u,v,w)=c(u,v)\), \(\sum_w c(v,w)=c(v)\), and \(\sum_w c(w)=c()\).
- Hold out part of the training set as “validation” data.
- Define \(c^{'}(w_1,w_2,w_3)\) to be the number of times the trigram \((w_1,w_2,w_3)\) is seen in the validation set.
- Take some small portion of all of our sentences, say 5%, as validation.
- We train on the 95% bigger portion.
- Define \(c^{'}\) as the number of times we see the training data in the smaller, other set.
- Choose \(\lambda_1, \lambda_2, \lambda_3\) to maximize:
\[L(\lambda_1,\lambda_2,\lambda_3) = \sum_{w_1,w_2,w_3} c^{'}(w_1,w_2,w_3)\;\textrm{log}\;q(w_3|w_1,w_2)\]
such that \(\lambda_1 + \lambda_2 + \lambda_3 = 1\) and \(\lambda_i \ge 0\;\forall\;i\) and where:
\(q(w_i|w_{i-2},w_{i-1}) =\)
\(\lambda_1 \times q_{ML}(w_i|w_{i-2},w_{i-1})\)
\(+\lambda_2 \times q_{ML}(w_i|w_{i-1})\)
\(+\lambda_3 \times q_{ML}(w_i)\)
- Many of the \(c^{'}(w_1,w_2,w_3)\) counts will of course be zero.
- Optimization problem to maximize L, under the contraints that the lambdas are positive and sum to one.
- If you maximize L it is easy to show that you minimize the perplexity of the language model with respect to the validation data.
- Take a function \(\Pi\) that partitions histories, e.g. for some bigram:
\[
\begin{equation}
\Pi(w_{i-2},w_{i-1}) = \begin{cases}
1, & \textrm{If Count}(w_{i-1},w_{i-2}) = 0\\
2, & \textrm{If 1} \le \textrm{Count}(w_{i-1},w_{i-2}) \le 2\\
3, & \textrm{If 3} \le \textrm{Count}(w_{i-1},w_{i-2}) \lt 5\\
4, & \textrm{Otherwise}
\end{cases}
\end{equation}
\]
- Introduce a dependence of the \(\lambda\)’s on the partition:
\[
\begin{align}
&\begin{aligned}
q(w_i\;|\;w_{i-2},w_{i-1}) & = \lambda_1^{\Pi(w_{i-2},w_{i-1})} \times q_{ML}(w_i\;|\;w_{i-2},w_{i-1}) \\
&\; + \lambda_2^{\Pi(w_{i-2},w_{i-1})} \times q_{ML}(w_i\;|\;w_{i-1}) \\
&\; + \lambda_3^{\Pi(w_{i-2},w_{i-1})} \times q_{ML}(w_i)
\end{aligned}
\end{align}
\]
- where \(\lambda_1^{\Pi(w_{i-2},w_{i-1})} + \lambda_2^{\Pi(w_{i-2},w_{i-1})} + \lambda_3^{\Pi(w_{i-2},w_{i-1})} = 1\), and \(\lambda_i^{\Pi(w_{i-2},w_{i-1})} \ge 0\;\forall\;i\).
- Instead of just 3 lambdas now we have 3 * 4 = 12 lambdas, one per MLE per partition, and we determine which parition to use based on the bigram count.
- We condition on the bigram counts.
- \(\lambda_1^1, \lambda_2^1, \lambda_3^1\). These counts are used if the bigram count is 0.
- \(\lambda_1^2, \lambda_2^2, \lambda_3^2\). These counts are used if the bigram count is [1, 2].
- \(\lambda_1^3, \lambda_2^3, \lambda_3^3\). These counts are used if the bigram count is [3, 5).
- \(\lambda_1^4, \lambda_2^4, \lambda_3^4\). These counts are used if the bigram count is [5, \(\infty\)).
- Partitions are generally chosen by hand, but this one is a typical definition.
- These 12 lambdas are optimized according to L as before using validation data.
- If this bigram count is 0 then parameter \(\lambda_1\) will also be equal to 0, else it is undefined.
- Recall that \(\lambda_1\) is for the trigram MLE, and the bigram count is in the denominator.
- Suppose we have a table of bigrams, their counts, and corresponding \(q_{ML}(w_i\;|\;w_{i-1})\).
| the |
48 |
|
| the, dog |
15 |
\(^{15}/_{48}\) |
| the, woman |
11 |
\(^{11}/_{48}\) |
| the, man |
10 |
\(^{10}/_{48}\) |
| the, park |
5 |
\(^{5}/_{48}\) |
| the, job |
2 |
\(^{2}/_{48}\) |
| the, telescope |
1 |
\(^{1}/_{48}\) |
| the, manual |
1 |
\(^{1}/_{48}\) |
| the, afternoon |
1 |
\(^{1}/_{48}\) |
| the, country |
1 |
\(^{1}/_{48}\) |
| the, street |
1 |
\(^{1}/_{48}\) |
- The MLEs are systematically high, especially if we have a large vocabulary. This is particularly true for the low count items.
In a sense these words that follow “the” are just lucky; what about those poor words that don’t appear after “the” in this data set but, in the “true” language, actually can appear after “the”?
Now define “discounted” counts, \(\textrm{Count}^{*}(x) = \textrm{Count}(x) - 0.5\)
| the |
48 |
|
|
| the, dog |
15 |
14.5 |
\(^{14.5}/_{48}\) |
| the, woman |
11 |
10.5 |
\(^{10.5}/_{48}\) |
| the, man |
10 |
9.5 |
\(^{9.5}/_{48}\) |
| the, park |
5 |
4.5 |
\(^{4.5}/_{48}\) |
| the, job |
2 |
1.5 |
\(^{1.5}/_{48}\) |
| the, telescope |
1 |
0.5 |
\(^{0.5}/_{48}\) |
| the, manual |
1 |
0.5 |
\(^{0.5}/_{48}\) |
| the, afternoon |
1 |
0.5 |
\(^{0.5}/_{48}\) |
| the, country |
1 |
0.5 |
\(^{0.5}/_{48}\) |
| the, street |
1 |
0.5 |
\(^{0.5}/_{48}\) |
- There is some missing or left over probability mass; if we sum the right-hand column you get \(\frac{43}{48} \lt 1\).
- The left over probability mass, in this case, is \(\frac{5}{48}\).
The essence of discounting is to take this left over probability mass and distribute it back to the words that do not appear after “the” in this data set.
We’ll define for any word \(w_{i-1}\) \(\alpha\), which is the left-over or missing probability mass:
\[\alpha(w_{i-1}) = 1 - \sum_{w} \frac{\textrm{Count}^{*}(w_{i-1},w)}{\textrm{Count}(w_{i-1})}\]
- e.g. in our example, \(\alpha(\textrm{the}) = 10 \times 0.5/48 = 5/48\).
Quiz: assume that we are given a corpus with the following properties:
- Count(the) = 70
- |{w: c(the, w) > 0}| = 15, i.e. there are 15 different words that follow “the”.
Furthermore assume that the discounted counts are defined as \(c^{*}(\textrm{the,w}) = c(\textrm{the,w}) - 0.3\). Under this corpus, what is the missing probability mass \(\alpha(\textrm{the})\) to 3dp?
\[
\begin{align}
&\begin{aligned}
\alpha(\textrm{the}) & = 1 - \sum_{w} \frac{\textrm{Count}^{*}(\textrm{the, w})}{\textrm{Count(the)}} \\
& = \frac{\textrm{Count(the)}}{\textrm{Count(the)}} - \frac{1}{\textrm{Count(the)}} \times \sum_{w} \textrm{Count}^{*}(\textrm{the,w}) \\
& = \frac{\textrm{Count(the)} - \sum_{w} \textrm{Count}^{*}\textrm{(the, w)}}{\textrm{Count(the)}} \\
& = \frac{\textrm{Count(the)} - \sum_{w} \left\{ \textrm{Count(the, w)} - 0.3\right\}}{\textrm{Count(the)}} \\
& = \frac{\textrm{Count(the)} + \sum_{w}(0.3) - \textrm{Count(the)}}{\textrm{Count(the)}} \\
& = \frac{0.3w}{\textrm{Count(the)}} \\
& = \frac{(0.3)(15)}{70} = 0.064\;\textrm{(3 dp)}
\end{aligned}
\end{align}
\]
- For a bigram model, define two sets
\[
\begin{align}
&\begin{aligned}
A(w_{i-1}) & = \left\{w : \textrm{Count}(w_{i-1},w) \gt 0\right\} \\
B(w_{i-1}) & = \left\{w : \textrm{Count}(w_{i-1},w) = 0\right\}
\end{aligned}
\end{align}
\]
- Assuming \(\alpha\) such that:
\[\alpha(w_{i-1}) = 1 - \sum_{w \in A(w_{i-1})} \frac{\textrm{Count}^{*}(w_{i-1},w)}{\textrm{Count}(w_{i-1})}\]
- And \(\textrm{Count}^{*}\) is such that:
\[\textrm{Count}^{*}(w_{i-1},w_i) = \textrm{Count}(w_{i-1},w_i) - \gamma\\ \textrm{where $\gamma$ is a constant}\]
\[
\begin{equation}
q_{BO}(w_i\;|\;w_{i-1}) = \begin{cases}
\frac{\textrm{Count}^{*}(w_{i-1},w_i)}{\textrm{Count}(w_{i-1})}, & \textrm{If } w_i \in A(w_{i-1})\\
\alpha(w_{i-1})\frac{q_{ML}(w_i)}{\sum_{w \in B(w_{i-1})} q_{ML}(w)}, & \textrm{If } w_i \in B(w_{i-1})
\end{cases}
\end{equation}
\]
- \(A(w_{i-1})\) is the set of words whose bigram count is greater than 0, so they follow e.g. “the”.
- \(B(w_{i-1})\) is the set of words whose bigram count is 0, so they’re never seen to follow e.g. “the”.
- \(\alpha(w_{i-1})\) is the missing probability mass.
- \(\frac{\textrm{Count}^{*}(w_{i-1},w_i)}{\textrm{Count}(w_{i-1})}\) is the discounted count for the words who are seen to follow e.g. “the”.
- If the word is never seen after e.g. “the”, rather than set its \(q(w_i|w_{i-1})\) parameter to 0 we assign it a portion of the missing probabiliy mass \(\alpha(w_{i-1})\), in proportion to its the unigram maximum-likelihood estimate \(q_{ML}(w_i)\) divided by the sum of all the unigram MLEs for other such words \(\sum_{w \in B(w_{i-1})} q_{ML}(w)\).
Quiz: Let’s return to a smaller version of our corpus:
- the book STOP
- his house STOP
This time we computer a bigram language model using Katz back-off with \(c^{*}(v,w) = c(v,w) - 0.5\).
What is the value of \(q_{BO}(\textrm{book | his})\) estimated from this corpus?
\[w_i = \textrm{book}, w_{i-1} = \textrm{his}\]
\[
\begin{align}
&\begin{aligned}
A(\textrm{his}) & = \textrm{{house}} \\
B(\textrm{his}) & = \textrm{{his, the, book, STOP}}
\end{aligned}
\end{align}
\]
Draw a table for \(w_{i-1}\) and all words that follow it, in order to determine \(\alpha(w_{i-1})\)
\[\alpha(\textrm{his}) = 1 - (0.5)/(1) = 0.5\]
Since \(\textrm{book} \in B(\textrm{his})\), i.e. since “book” never follows “his” in the corpus:
\[
\begin{align}
&\begin{aligned}
\sum_{w \in B(w_{i-1})} q_{ML}(w) & = q_{ML}(\textrm{his}) + q_{ML}(\textrm{the}) + q_{ML}(\textrm{book}) + q_{ML}(\textrm{STOP}) \\
& = (1/6) + (1/6) + (1/6) + (2/6) \\
& = 5/6
\end{aligned}
\end{align}
\]
\[
\begin{align}
&\begin{aligned}
q_{BO}(\textrm{book | his}) & = \alpha(w_{i-1})\frac{q_{ML}(w_i)}{\sum_{w \in B(w_{i-1})} q_{ML}(w)} \\
& = (0.5) \times \frac{(1/6)}{(5/6)} \\
& = 0.1
\end{aligned}
\end{align}
\]
- For a trigram model, first define two sets
\[
\begin{align}
&\begin{aligned}
A(w_{i-2},w_{i-1}) & = \left\{w : \textrm{Count}(w_{i-2},w_{i-1},w) \gt 0\right\} \\
B(w_{i-2},w_{i-1}) & = \left\{w : \textrm{Count}(w_{i-2},w_{i-1},w) = 0\right\}
\end{aligned}
\end{align}
\]
- A trigram model is defined in terms of the bigram model:
\[
\begin{equation}
q_{BO}(w_i\;|\;w_{i-2},w_{i-1}) = \begin{cases}
\frac{\textrm{Count}^{*}(w_{i-2},w_{i-1},w_i)}{\textrm{Count}(w_{i-2},w_{i-1})}, & \textrm{If } w_i \in A(w_{i-2},w_{i-1})\\
\alpha(w_{i-2},w_{i-1})\frac{q_{BO}(w_i|w_{i-1})}{\sum_{w \in B(w_{i-2},w_{i-1})} q_{BO}(w|w_{i-1})}, & \textrm{If } w_i \in B(w_{i-2},w_{i-1})
\end{cases}
\end{equation}
\]
where
\[\alpha(w_{i-2},w_{i-1}) = 1 - \sum_{w \in A(w_{i-2},w_{i-1})} \frac{\textrm{Count}^{*}(w_{i-2},w_{i-1},w)}{\textrm{Count}(w_{i-2},w_{i-1})}\]
- The one variable is the discount constant. It is typically between 0 and 1, and it can also be chosen via optimization on a validation data set.
- Three steps in deriving the language model probabilities:
- Expand \(p(w_1, w_2, \ldots, w_n)\) using Chain Rule.
- Make Markov Independence Assumptions, i.e. \(p(w_i\;|\;w_1, w_2, \ldots, w_{i-2}, w_{i-1}) = p(w_i\;|\;w_{i-2},w_{i-1})\)
- Smooth the estimates using low order counts; linear interpolation and discounting.
- Other methods used to improve language models
- “Topic” or “long-range” features.
- Condition on the topic of the document within which sentences belong.
- Condition on words outside of the two-word window under the second-order Markov assumption.
- Syntactic models
- It’s generally hard to improve on trigram models though!
- We’d like to model pairs of sequences, rather than just one sequence.
- The general problem is the sequence labelling problem, aka the tagging problem.
Two instances of this problem - POS tagging and named entity recognition.
- Part-of-Speech Tagging: a fundamental problem.
- Input: sentence.
- Output: a tag sequence, aka a state sequence.
Input, some sequence of words, a sentence:
Profits soared at Boeing Co., easily topping forecasts on Wall
Street, as their CEO Alan Nulally announced first quarter
results.
N = Noun
V = Verb
P = Preposition
Adv = Adverb
Adj = Adjective
...
Profits/N soared/V at/P Boeing/N Co./N ,/, easily/ADV
topping/V forecasts/N on/P Wall/N Street/N ,/, as/P
their/POSS CEO/N Alan/N Mulally/N announced/V first/ADJ
quarter/N results/N ./.
- But context matters.
profits isn’t always a noun, it can sometimes be a verb.topping is a verb, but can sometimes be a noun.- …
- Also, individual words, regardless of context, have a preference for their part of speech.
quarter can be a noun or a verb, but in general is more likely to be a noun.
- Also some words are very rare, and may not show up in the training data.
- Important to be able to deal with this.
- Named Entity Recognition
- Input: a sentence.
- Output: identify names and their type (company, location, person, …)
- Input: same as above
- Output:
Profits soared at [Company: Boeing Co.], easily ...
[Location: Wall Street], ..., [Person: Alan Mulally]
- At first blush named entity recognition looks like segmentation, not part-of-speech tagging. But really they’re the same.
- Input: same as above
- Tags:
NA = No entity
SC = Start Company
CC = Continue Company
SL = Start Location
CL = Continue Location
...
Profits/NA soared/NA at/NA Boeing/SC Co./CC ,/NA easily/NA
topping/NA ... Wall/SL Street/CL ,/NA ... CEO/NA Alan/SP
Mulally/CP ...
- We are encoding the named entity boundaries as a tag sequence.
Quiz: given sentence: Profits are topping all estimates.
We also know:
Profits can be N or V.are is Vtopping can be N, ADJ, or V.all can be DT, ADV, or N.estimates can be N or V.
How many tag sequences are possible?
\[= 2 \times 1 \times 3 \times 3 \times 2 = 36\]
- Objective: treating this like a supervised machine learning problem
- Use a very common resource, called the “Wall Street Journal Treebank”.
- Features: sentences (not individual words).
- Training set: 38,219 sentences, each with tagged words.
- Label: a sentence with each word tagged.
- !!AI there are a lot of tags here. A reference list of tags is available in the Penn Treebank Tags.
- Output: a functon that maps sentences to tagged words.
- There are now many corpora available, across many languages.
Influential/JJ members/NNS of/IN ... bailout/NN agency/NN
can/MD raise/VB capital/NN ./.
- What will help us in this problem? Two constraints:
- Local: e.g. can is more likely to be a modal verb (MD) than a noun (NN).
- A modal verb (MD) is an auxillary verb used to indicate likelihood, ability, permission, and obligation.
- Contextual: e.g. a noun (NN) is more likely than a verb (VB*) to follow a determiner (DT).
- (e.g.
the can is more likely to refer to a can of soup than talk about the’s ability to do something)
- A determiner (DT) is a word, phrase, or affix that occurs together with a noun (NN).
- DT can be indefinite articles (
the, a, an), demonstratives (this, that), quantifiers (many, few, several).
- Recall that an affix is a morpheme that attaches to word stems. Can be prefix, suffix, infix (in the middle of a word) or circumfix (on both sides of the word)
- Sometimes the contraints are in conflict:
The trash can is in the garage.
can has a local preference to be a modal verb (MD) because it follows a noun.- But clearly
can belongs as a whole with trash can, so it depends on context.
- We can build a model that balances these two contraints.
- We have training examples \(x^{(i)}, y^{(i)}\) for \(i = 1 \ldots m\).
- Each \(x^{(i)}\) is an input, each \(y^{(i)}\) is a label.
- Objective: learn a function \(f\) that maps inputs \(x\) to labels \(f(x)\).
- e.g.
\[
\begin{align}
&\begin{aligned}
& x^{(1)} = \textrm{the dog laughs}, & y^{(1)} = \textrm{DT NN VB} \\
& x^{(2)} = \textrm{the dog barks}, & y^{(2)} = \textrm{DT NN VB} \\
& \ldots & \ldots
\end{aligned}
\end{align}
\]
- The first model you may consider is a conditional model.
- Learn a distribution \(p(y|x)\) from training examples.
- For any test input \(x\), define \(f(x) = \textrm{arg max}_{y}p(y|x)\).
- The \(y\) that maximizes this conditional probability.
- Input \(x\), search through all possible \(y\)’s, return most likely \(y\).
- Alternative are generative models.
- Same problem.
- Learn a joint distribution \(p(x,y)\) from training examples.
- Before we had \(p(y|x)\).
- Often we have \(p(x,y)\) = \(p(y)p(x|y)\).
- Bayes Rule.
- \(p(y)\) is the prior probability; how likely is \(y\) a-priori?
- \(p(x|y)\) is the conditional probability. Given \(y\) how likely is \(x\)?
- Note: by the total probability variant of Bayes Rule we have:
\[p(y|x) = \frac{p(y)p(x|y)}{p(x)}\]
\[p(x) = \sum_y p(y)p(x|y)\]
- Estimating \(p(y|x)\) directly is often referred to as a discriminative model.
- We will see a lot of discriminative models later in the course.
- Estimating \(p(x,y)\) is a generative model.
- There are pros and cons to each, a lot of research, back and forth.
- Still confused about generative vs. discriminative? http://stackoverflow.com/questions/879432/what-is-the-difference-between-a-generative-and-discriminative-algorithm
- A generative algorithm takes into account some model about how the data was generated, and then classifies the input.
- By calculating \(p(x,y)\) we have enough to shove it into Bayes’ rule in order to generate \(p(y|x)\).
- However, if we want, we can generate more \((x,y)\) that fit the model.
- A discriminative model doesn’t care and just classifies.
- Given some input it discerns what’s necessary to map it onto the most likely output.
- How do we apply a generative model to a new test example?
- Output from the model:
\[
\begin{align}
&\begin{aligned}
f(x) & = \textrm{argmax}_{y}\;p(y|x) \\
& = \textrm{argmax}_{y}\;\frac{p(y)p(x|y)}{p(x)} \\
& = \textrm{argmax}_{y}\;p(y)p(x|y)
\end{aligned}
\end{align}
\]
- Second line: assuming we have a generative model, by Bayes Rule.
- Third line: \(p(x)\) does not vary with \(y\). \(\textrm{argmax}\) implies we’re searching over \(y\), but denominator is constant and hence we can discard it.
- This is computationally very useful, can be expensive to calculate.
- Models that decompose the joint probability \(p(x,y)\) into \(p(y)\) and \(p(x|y)\) are called noisy-channel models.
- Intuitively, the input \(x\) is generated in two steps.
- Label \(y\) is chosen with probability \(p(y)\).
- Input \(x\) is generated from the distribution \(p(x|y)\).
- We have an input sentence \(x = x_1, x_2, \ldots, x_n\). (\(x_i\) is the \(i\)’th word in the sentence).
- We have a tag sequence \(y = y_1, y_2, \ldots, y_n\). (\(y_i\) is the \(i\)’th tag in the sentence).
- We’ll use an HMM to define:
\[p(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n)\]
- for any sentence \(x_1 \ldots x_n\) and tag sequence \(y_1 \ldots y_n\) of the same length.
- Note this is generative (\(p(x,y)\)), not discriminative (\(p(y|x)\)).
- Think of the \(x_i\) as an input and the \(y_i\) as a label.
- Then the most likely tag sequence for \(x\) is:
\[\textrm{arg}\underset{y_1 \ldots y_n}{\textrm{max}} p(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n)\]
- The number of total possible sequences is \(O(2^n)\), so brute force search is not feasible.
- For any sentence \(x_1, x_2, \ldots, x_n\), where \(x_i \in V\) for \(i = 1, 2, \ldots, n\), and
- For any tag sequence \(y_1, y_2, \ldots, y_{n+1}\), where \(y_i \in S\) for \(i = 1, 2, \ldots, n\) and \(y_{n+1} = \textrm{STOP}\).
- The joint probability of the sentence and tag sequence is:
\[p(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_{n+1}) = \prod_{i=1}^{n+1} q(y_i|y_{i-2},y_{i-1}) \prod_{i=1}^{n} e(x_i|y_i)\]
- An example of the joint probability could be \(p(\textrm{the, dog barks, DT, NN, VB, STOP})\).
- The first product is a trigram model applied to tag sequences! Very similar to before.
- One \(q\) term for each tag including the STOP symbol.
- The second product could have e.g. \(e(\textrm{the | DT})\) is the probability of a tag emitting or generating a word.
- One \(e\) term for each (tagged) word.
- where we’ve assumed, as before in Markov Models, that \(y_0 = y_{-1} = {*}\) (the start symbol).
- \(V\) is the set of possible words in the language, e.g. \(\{\textrm{the, dog, book, ate, his}\}\)
- \(S\) is the set of possible tags, e.g. \(\{\textrm{DT, NN, VB, P, ADV, ...}\}\).
- \(\simeq\) hundreds of tags; the Wall Street Journal courpus has \(\simeq\) 50 tags.
- Parameters of the model:
- \(q(s|u,v)\;\forall\;s \in S \cup \{\textrm{STOP}\},\;u,v \in S \cup \{\textrm{*}\}\)
- Trigram parameters (but referred to in a quiz as transition parameters).
- \(e(x|s)\;\forall\;s \in S, x \in V\)
- This model has the same form as a noisy-channel model.
- The first \(q\) parameters are the prior probability of the tags, i.e. \(p(y)\).
- The second \(e\) parameters are the conditional probabilities, i.e. \(p(x|y)\).
- Notice that the \(e\) parameters have an independence assumption.
- Any value for random variable \(X_i = x_i\) is only dependent on \(Y_i = y_i\).
- More formally given the value of \(Y_i\) the value for \(X_i\) is conditionally independent of both previous observations \(X_1 \ldots X_{i-1}\) and other state values \(Y_1 \ldots Y_{i-1}, Y_{i+1}, \ldots Y_{n+1}\).
- See notes p12.
- Useful thinking exercise - how do I generate sequence pairs \(y_1, \ldots, y_{n+1}, x_1, \ldots, x_n\)?
- Initialize \(i=1\) and \(y_0 = y_{-1} = \textrm{*}\).
- Generate \(y_i\) from distribution \(q(y_i|y_{i-2},y_{i-1})\).
- If \(y_i = \textrm{STOP}\) then return \(y_1 \ldots y_i, x_1 \ldots x_{i-1}\). Else, generate \(x\) from distribution \(e(x_i|y_i)\).
- Set \(i=i+1\), return to step 2.
Quiz: Given tagset \(S = \{\textrm{D, N}\}\), a vocabulary \(V = \{\textrm{the, dog}\}\), and a HMM with transition parameters:
- \(q(\textrm{D | *, *}) = 1\)
- \(q(\textrm{N | *, D}) = 1\)
- \(q(\textrm{STOP | D, N}) = 1\)
- \(q(s|u,v) = 0\) for all other \(q\) params.
and emission parameters:
- \(e(\textrm{the | D}) = 0.9\)
- \(e(\textrm{dog | D}) = 0.1\)
- \(e(\textrm{dog | N}) = 1\)
Under this model how many pairs of sequences \(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_{n+1}\) satisfy \(p(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_{n+1}) \gt 0\)?
First: how many non-zero-probability tag sequences are there? Enumerate them by drawing a graph of nodes and edges, where a node is a word and an edge is labelled with the transition probability to another word. Then follow all paths from any start symbol to any stop symbol whose product of probabilities is \(\gt\) 0.
D, N, STOP
There’s only one! OK. Refer back to your taq sequence graph and copy it for each possible word that a given tag (i.e. node) that it may “generate”. If e.g. N could generate two words, not one, we would have four possible sentences.
the dog
dog dog
There’s only two! OK. Hence the answer itself is two, because we have just generated a sentence for each possible (tag, word) pair.
If we have:
- \(n = 3\),
- The sentence \(\{x_1, x_2, x_3\} = \{\textrm{the, dog, laughs}\}\), and
- The tag sequence \(\{y_1, y_2, y_3, y_4\} = \{\textrm{D, N, V, STOP}\}\).
Then:
\[
\begin{align}
&\begin{aligned}
& p(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_{n+1}) \\
= & q(\textrm{D | *, *}) \times q(\textrm{N | *, D}) \times q(\textrm{V | D, N}) \times q(\textrm{STOP | N, V}) \times \\
& e(\textrm{the | D}) \times e(\textrm{dog | N}) \times e(\textrm{laughs | V})
\end{aligned}
\end{align}
\]
- STOP is a special tag that terminates the sequence.
- We take \(y_0 = y_{-1} = \textrm{*}\), where \(\textrm{*}\) is a special “padding” symbol.
- The \(e\) parameters can be interpreted as the conditional probability \(p(\textrm{the dog laughs | D N V STOP})\).
Quiz: given set \(S = \{\textrm{D, N, V}\}\), and vocabulary \(V = \{\textrm{the, cat, drinks, milk, dog}\}\), and an HMM model:
- transition parameters \(q(s|u,v) = \frac{1}{4}\;\forall\;s, u, v\)
- generative parameters \(e(x|s) = \frac{1}{5}\;\forall\; \textrm{tags}\;s\;\textrm{and words}\;x\).
What is the value, under this model, of:
\[p(\textrm{the, cat, drinks, milk, D, N, V, N, STOP})\]
\[
\begin{align}
&\begin{aligned}
& p(\textrm{the, cat, drinks, milk, STOP, D, N, V, N}) \\
= & \prod_{i=1}^{n+1} q(y_i|y_{i-2},y_{i-1}) \prod_{i=1}^{n} e(x_i|y_i) \\
= & \{ p(\textrm{the | *, *}) \times p(\textrm{cat | *, the}) \times p(\textrm{drinks | the, cat}) \times p(\textrm{milk | cat, drinks}) \times p(\textrm{STOP | drinks, milk}) \} \times \\
& e(\textrm{the | D}) \times e(\textrm{cat | N}) \times e(\textrm{drinks | V}) \times e(\textrm{milk | N}) \\
= & \left(\frac{1}{4}\right)^5 \times \left(\frac{1}{5}\right)^4
\end{aligned}
\end{align}
\]
- The first product is a second-order Markov Chain
- Recall \(p(x,y) = p(y) \times p(x|y)\)
- This product is solving for \(p(y)\).
- The second project is \(x_j\)’s being observed.
- Strong independence assumption that each word depends only on its underlying, generating tag.
- The generative process: we choose a sequence of tags, and then for each tag generate an associated word.
- The \(y\)’s are not observed.
- The \(x\)’s are observed.
- And so we will flip this: given an observation find the most likely underlying (hidden) tag sequence.
Quiz: for a bigram HMM:
\[p(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n) = \prod_{i=1}^{n+1} q(y_i|y_{i-1}) \prod_{i=1}^{n} e(x_i|y_i)\]
e.g.
\[
\begin{align}
&\begin{aligned}
q(\textrm{Vt | DT, JJ}) & = \lambda_1 \times \frac{\textrm{Count(Dt, JJ, Vt)}}{\textrm{Count(Dt, JJ)}} \\
& + \lambda_2 \times \frac{\textrm{Count(JJ, Vt)}}{\textrm{Count(JJ)}} \\
& + \lambda_3 \times \frac{\textrm{Count(Vt)}}{\textrm{Count()}}
\end{aligned}
\end{align}
\]
\[\lambda_1 + \lambda_2 + \lambda_3 = 1\] \[\forall\;i, \lambda_i \ge 0\]
\[e(\textrm{base | Vt}) = \frac{\textrm{Count(Vt, base)}}{\textrm{Count(Vt)}}\]
- For trigram / transition parameters:
- We can of course induce counts of tag sequences directly from our corpus, and then determine maximum-likelihood estimates.
- \(\lambda_1\) for trigram MLE.
- \(\lambda_2\) for bigram MLE.
- \(\lambda_3\) for unigram MLE.
- Linear interpolation is used, as seen before.
- For emission parameters:
- One problem.
- \(e(x|y) = 0\;\forall\;y\) if \(x\) is never seen in the training data.
- !!AI sounds familiar! Will we do Laplacian smoothing, we we “add fudge” to everything, or back-off smoothing, where high mass gets re-distributed to zero mass, or something else?
Quiz: Given the following corpus:
- the dog barks -> D N V STOP
- the cat sings -> D N V STOP
Assume we’ve calculated MLEs of a trigram HMM from this data. What is the value of the emission parameter \(e(\textrm{cat | N})\) from this HMM?
\[
\begin{align}
&\begin{aligned}
e(\textrm{cat | N}) = & \frac{\textrm{Count(N, cat)}}{\textrm{Count(N)}} \\
= & \frac{(1)}{(2)}
\end{aligned}
\end{align}
\]
Say we estimate the transition parameters for a trigram HMM using linear interpolation, such that \(\lambda_i = \frac{1}{3}\) for \(i = \{1, 2, 3\}\). What is the value of the transition parameter \(q(\textrm{STOP | N, V})\) under this model?
\[
\begin{align}
&\begin{aligned}
q(\textrm{STOP | N, V}) = & \lambda_1 \times \frac{\textrm{Count(N, V, STOP)}}{\textrm{Count(N, V)}} \\
+ & \lambda_2 \times \frac{\textrm{Count(V, STOP)}}{\textrm{Count(V)}} \\
+ & \lambda_3 \times \frac{\textrm{Count(STOP)}}{\textrm{Count()}} \\
= & \left(\frac{1}{3} \times \frac{(2)}{(2)}\right) \\
+ & \left(\frac{1}{3} \times \frac{(2)}{(2)}\right) \\
+ & \left(\frac{1}{3} \times \frac{(2)}{(8)}\right) \\
= & 0.75
\end{aligned}
\end{align}
\]
Profits soared at Boeing Co., easily topping ...
CEO Alan Mulally.
topping and Mulally are likely to be infrequent.- Long tail: you will frequently encounter words in test data that you have never encountered in training data.
- And hence: \(e(\textrm{Mulally | y}) = 0\) for all tags \(y\).
- And it can be verified that the joint probability \(p(x_1, \ldots, x_n, y_1, \ldots, y_{n+1}) = 0\) for all tag sequences \(y_1, \ldots, y_{n+1}\).
- This is because all tag sequences will involve this emission parameter.
And hence all tag sequences are equally likely; applying argmax to an expression that always evaluates to zero implies that \(y\) is equally maximum everywhere!
- A common way of dealing with this:
- Split the vocabulary into two sets.
- Frequent words: words occurring \(\ge\) 5 times in training (or some threshold).
- Low frequency words: all other words.
- Map low frequency words into a small, finite set, depending on affixes.
- The set of low frequency words is very large.
Map each low frequency word to a small set of e.g. 20 new words.
from [Bikel et. al 1999] for named-entity recognition.
| twoDigitNum |
90 |
Two digit year |
| fourDigitNum |
1990 |
Four digit year |
| containsDigitAndAlpha |
A8956-67 |
Product code |
| containsDigitAndDash |
09-96 |
Date |
| containsDigitAndSlash |
11/9/89 |
Date |
| containsDigitAndComma |
23,000.00 |
Monetary amount |
| containsDigitAndPeriod |
1.00 |
Monetary, financial |
| othernum |
456789 |
Other |
| allCaps |
BBN |
Organization |
| capsPeriod |
M. |
Initial |
| firstWord |
first |
no useful capitalisation infomation |
| initCap |
Sally |
Capitalized word |
| lowercase |
can |
Uncapitalized word |
| other |
, |
Punctuation, other words |
- These were chosen by hand with intuition.
- We want to preserve some useful information for the specific task at hand, i.e. named entity recognition.
- e.g.
firstWord will be capitalized in the corpus, but we lowercase it because the capitalization does not give us useful information, because all words at the start of a sentence are capitalized.
- We’re mapping low-frequency words to classes that preserve spelling features.
Return to an old example. Before transformation:
Profits/NA soared/NA at/NA Boeing/SC Co./CC easily/NA
topping/NA forecasts/NA on/NA Wall/SL Street/CL ,/NA their/NA
CEO/NA Alan/SP Mulally/CP announced/NA first/NA quarter/NA
results/NA ./NA
After transformation:
firstword/NA soared/NA at/NA initCap/SC Co./CC ,/NA easily/NA
lowercase/NA forecasts/NA on/NA initCap/SL Street/CL ,/NA as/NA
their/NA CEO/NA Alan/SP initCap/CP announced/NA first/NA
quarter/NA results/NA ./NA
- Resolving low-frequency words in a way that preserves their spelling is useful for the named-entity recognition problem.
- Build our HMM on this transformed data.
- \(e(\textrm{firstword | NA})\)
- \(e(\textrm{initCap | SC})\)
- We’re closing the vocabulary.
- This is a simple method, but requires human heuristics.
- How to apply HMMs to new test sentences?
- For a new test input sentence \(x_1, \ldots, x_n\), map it onto the most likely set of tags, i.e. find:
\[\textrm{arg}\underset{y_1 \dots y_{n+1}}{\textrm{max}} p(x_1 \ldots x_n, y_1 \ldots y_{n+1})\]
where the arg max is taken over all sequences \(y_1 \ldots y_{n+1}\) such that \(y_i \in S\) for \(i = 1, \ldots, n\) and \(y_{n+1} = \textrm{STOP}\).
We assume that \(p\) again takes the form:
\[p(x_1 \ldots x_n, y_1 \ldots y_{n+1}) = \prod_{i=1}^{n+1} q(y_i | y_{i-2}, y_{i-1}) \prod_{i=1}^{n} e(x_i | y_i)\]
\[\textrm{arg}\underset{y_1 \dots y_{n+1}}{\textrm{max}} p(x_1 \ldots x_n, y_1 \ldots y_{n+1}) = \textrm{arg}\underset{y_1 \dots y_{n+1}}{\textrm{max}} \textrm{log} \left\{ p(x_1 \ldots x_n, y_1 \ldots y_{n+1}) \right\}\]
- And to clarify what I mean by add instead of multiply:
\[
\begin{align}
&\begin{aligned}
p(x_1 \ldots x_n, y_1 \ldots y_{n+1}) & = \prod_{i=1}^{n+1} q(y_i | y_{i-2}, y_{i-1}) \prod_{i=1}^{n} e(x_i | y_i) \\
\textrm{log} \left\{ p(x_1 \ldots x_n, y_1 \ldots y_{n+1}) \right\} & = \textrm{log} \left\{ \prod_{i=1}^{n+1} q(y_i | y_{i-2}, y_{i-1}) \prod_{i=1}^{n} e(x_i | y_i) \right\} \\
& = \textrm{log} \left\{ \prod_{i=1}^{n+1} q(y_i | y_{i-2}, y_{i-1}) \right\} + \textrm{log} \left\{ \prod_{i=1}^{n} e(x_i | y_i) \right\}
\end{aligned}
\end{align}
\]
\[
\begin{align}
&\begin{aligned}
& = \textrm{log} \left\{ q(y_1|y_{-1},y_0) \times q(y_2|y_0,y_1) \times \ldots \times q(y_{n+1}|y_{n-1},y_{n}) \right\} \\
& + \textrm{log} \left\{ e(x_0|y_0) \times e(x_1|y_1) \times \ldots \times e(x_n|y_n) \right\} \\
& = \textrm{log} \left\{ q(y_1|y_{-1},y_0) \right\} + \textrm{log} \left\{ q(y_2|y_0,y_1) \right\} + \ldots + \textrm{log} \left\{ q(y_{n+1}|y_{n-1},y_{n}) \right\} \\
& + \textrm{log} \left\{ e(x_0|y_0) \right\} + \textrm{log} \left\{ e(x_1|y_1) \right\} + \ldots + \textrm{log} \left\{ e(x_n|y_n) \right\}
\end{aligned}
\end{align}
\]
- To be absolutely clear: it is irrelevant what base you use in the logarithm.
- In this course I think we’re expected to use base 2.
- In the ARPA file format of backoff language models base 10 is used.
- But use whatever you want! Just don’t forget which one you used ;).
- For example
- \(x_1 \ldots x_n = \{\textrm{the, dog, laughs}\}\).
- \(y_1 \ldots y_n = \{\textrm{D, N, V}\}\) (the correct answer).
- \(S = \{\textrm{D, N, V}\}\) (assume that the set of all possible tags is just this).
- So \(|S| = 3\), and all possible tag sequences are all combinations (not permutations):
- D D D STOP
- D D N STOP
- D D U STOP
- D U D STOP
- …
- Only \(3^3 = 27\) possible tag sequences.
- Use the transmission and emissions parameters of the HMM model to assign probabilities to each particular tag sequnce, then choose the most likely tag sequence.
However, in the general case \(|S|^n\), where \(n\) is sentence length, is the number of possible sequences.
- The transmission parameters only depend on sequences of length three for trigram HMMs.
- This structure allows a more efficient solution.
- Define \(n\) to be length of sentence.
- Define \(S_k\) for \(k = -1, 0, \ldots, n\), to be set of possible tags at position \(k\):
\[S_{-1} = S_0 = \{\textrm{*}\}\] \[S_k = S\;\textrm{for}\;k \in \{1, 2, \ldots n\}\]
\[r(y_{-1}, y_0, y_1, \ldots, y_k) = \prod_{i=1}^{k} q(y_i | y_{i-2}, y_{i-1}) \prod_{i=1}^{k} e(x_i|y_i)\]
- Note that, always, \(y_{-1} = y_0 = \{\textrm{*}\}\).
- This is a truncated \(q\), as it only goes \(i=1\) to \(k\).
- Define a dynamic programming table
\[\pi(k,u,v) = \textrm{maximum probability of a tag sequence ending in tags}\;u, v\;\textrm{at position}\;k\]
i.e.
\[\pi(k,u,v) = max_{(y_{-1},y_0,y_{1},\ldots,y_k):y_{k-1}=u,\;y_k=v} r(y_{-1},y_0,y_1,\ldots,y_k)\]
- \(k\) takes any value \(\{\textrm{1,2,...,n}\}\).
- \(u \in S_{k-1}\).
\(v \in S_k\).
- What do the \(S\) and \(k\) expressions at the begining imply:
- For example, (the, dog, laughs, D, N, V) implies \(k = 3\).
- Each tag in \(S\) could be responsible for generating a word in \(x\).
- If \(S = \{\textrm{D, N, V, P}\}\), then \(x_1\) could be one of D, N, V, P, as is \(x_2\), etc.
\[\underset{-1}{\textrm{*}}\;\underset{0}{\textrm{*}}\;\underset{1}{\textrm{The}}\;\underset{2}{\textrm{man}}\;\underset{3}{\textrm{saw}}\;\underset{4}{\textrm{the}}\;\underset{5}{\textrm{dog}}\;\underset{6}{\textrm{with}}\;\underset{7}{\textrm{the}}\;\underset{8}{\textrm{telescope}}\;\]
- Assume \(S = \{\textrm{D, N, V, P}\}\)
- What does \(\pi(7, \textrm{P}, \textrm{D})\) mean, intuitively?
- The probability of the most likely tag sequence ending at the word in position 7 such that the last two tags are (P, D).
- Fix ‘with’ (6) to P.
- Fix ‘the’ (7) with D.
- Each preceding word has four possible tags.
- ‘dog’ (5) could be D, N, V, P.
- ‘the’ (4) could be D, N, V, P.
- ‘saw’ (3) could be D, N, V, P.
- ‘man’ (2) could be D, N, V, P.
- ‘The’ (1) could be D, N, V, P.
Quiz: We have a trigram HMM model with the following transition parameters:
- \(q(\textrm{D | *, *}) = 1\)
- \(q(\textrm{N | *, D}) = 1\)
- \(q(\textrm{V | D, N}) = 1\)
- \(q(\textrm{STOP | N, V}) = 1\)
and emission parameters:
- \(e(\textrm{the | D}) = 0.8\)
- \(e(\textrm{dog | D}) = 0.2\)
- \(e(\textrm{dog | N}) = 0.8\)
- \(e(\textrm{the | N}) = 0.2\)
- \(e(\textrm{barks | V}) = 1.0\)
Say we have the sentence:
the dog barks
What is the value of \(\pi(3, \textrm{N}, \textrm{V})\)?
- Intuitively, this reads as ‘what is the probability of the most likely tag sequence that ends at position 3 such that the last two tags are N and V?’
- First, expand and label your test sentence, omitting the STOP symbol:
\[\underset{-1}{\textrm{*}}\;\underset{0}{\textrm{*}}\;\underset{1}{\textrm{the}}\;\underset{2}{\textrm{dog}}\;\underset{3}{\textrm{barks}}\]
\[
\begin{align}
&\begin{aligned}
r(y_{-1},y_0,y_1,\ldots,y_n) & = \prod_{i=1}^{k} q(y_i|y_{i-2},y_{i-1}) \prod_{i=1}^{k} e(x_i|y_i) \\
r(\textrm{*, *, D, N, V}) & = \left\{ q(\textrm{D | *, *}) \times q(\textrm{N | *, D}) \times q(\textrm{V | D, N}) \right\} \times \\
& \left\{ e(\textrm{the | D}) \times e(\textrm{dog | N}) \times e(\textrm{barks | V}) \right\} \\
& = \left\{ 1 \times 1 \times 1\right\} \times \left\{0.8 \times 0.8 \times 1.0 \right\} \\
& = 0.64
\end{aligned}
\end{align}
\]
- Base case: \(\pi(0, \textrm{*}, \textrm{*}) = 1\)
- Every tag sequence starts with \(\textrm{* *}\).
- Recursive definition: \(\forall\; k \in \{1 \ldots n\},\;\forall\; u \in S_{k-1}\;\textrm{and}\;v \in S_k:\)
\[\pi(k,u,v) = \underset{w \in S_{k-2}}{\textrm{max}} (\pi(k-1),w,u) \times q(v|w,u) \times e(x_k|v))\]
- \(u\) can take any tag in \(S_{k-1}\), \(v\) can take any tag in \(S_k\).
- Notice how we’re working backwards in the sentence back to the base case, the start.
(part 2)
\[\underset{-1}{\textrm{*}}\;\underset{0}{\textrm{*}}\;\underset{1}{\textrm{The}}\;\underset{2}{\textrm{man}}\;\underset{3}{\textrm{saw}}\;\underset{4}{\textrm{the}}\;\underset{5}{\textrm{dog}}\;\underset{6}{\textrm{with}}\;\underset{7}{\textrm{the}}\;\underset{8}{\textrm{telescope}}\;\]
What is \(\pi(7, P, D)\)?
- Recall this puts ‘with’ (6) = P, ‘the’ (7) = D.
- \(u = \textrm{P}, v = \textrm{D}\)
- Note that \(S_5 = S_4 = \ldots = S = \{\textrm{D, N, V, P}\}\).
\[
\begin{align}
&\begin{aligned}
\pi(7, \textrm{P}, \textrm{D}) = & \underset{w \in \{\textrm{D,N,V,P}\}}{\textrm{max}} \left\{ \pi(6, w, \textrm{P}) \times q(\textrm{D} | w, \textrm{P}) \times e(\textrm{the} | \textrm{D}) \right\}
\end{aligned}
\end{align}
\]
- Any tag sequence ending in (P, D) must have included one previous tag in (D, N, V, P). The ‘max’ explicitly searches over these.
Quiz: assume \(S = \{\textrm{D, N, V, P}\}\) and a trigram HMM with parameters:
- \(q(\textrm{D | N, P}) = 0.4\)
- \(q(\textrm{D | w, P}) = 0\) for \(w \neq N\).
- \(e(\textrm{the | D}) = 0.6\)
We are also given the sentence:
Ella walks to the red house
Say the dynamic programming table for this sentence has the following entries:
- \(\pi(\textrm{3, D, P}) = 0.1\)
- \(\pi(\textrm{3, N, P}) = 0.2\)
- \(\pi(\textrm{3, V, P}) = 0.01\)
- \(\pi(\textrm{3, P, P}) = 0.5\)
What is the value of \(\pi(\textrm{4, P, D})\)?
- \(u = \textrm{P}\)
- \(v = \textrm{D}\)
\[
\begin{align}
&\begin{aligned}
\pi(k,u,v) = & \underset{w \in S_{k-2}}{\textrm{max}} (\pi(k-1),w,u) \times q(v|w,u) \times e(x_k|v)) \\
\pi(4, \textrm{P}, \textrm{D}) = & \underset{w \in \{\textrm{D, N, V, P}\}}{\textrm{max}} \left\{ \pi(3, w, \textrm{P}) \times q(\textrm{D} | w, \textrm{P}) \times e(\textrm{the | D}) \right\} \\
= & \textrm{max} \left\{ 0.1 \times 0 \times 0.6, 0.2 \times 0.4 \times 0.6, 0.01 \times 0 \times 0.6, 0.5 \times 0 \times 0.6 \right\} \\
= & 0.048
\end{aligned}
\end{align}
\]
- Inputs:
- a sentence \(x_1 \ldots x_n\), a sequence of words
- transmisson parameters \(q(s|u,v)\),
- emission parameters \(e(x|s)\).
- Output:
- \(\underset{y_1 \ldots y_{n+1}}{\textrm{max}} p(x_1 \ldots x_n, y_1 \ldots y_{n+1})\)
- Notice this is not argmax; just returns max probability. A simple change later will fix this.
- Initializtion:
- Set \(\pi(0,\textrm{*},\textrm{*}) = 1\).
- Base case of the recursion.
- Definition:
- \(S_{-1} = S_0 = \{\textrm{*}\}\)
- Can only have the star symbols at positions -1 and 0.
- \(S_k = S\;\forall\;k \in \{1 \ldots n\}\)
- Algorithm
- For \(k = 1 \ldots n\):
- For \(u \in S_{k-1}\), \(v \in S_k\):
- \(\pi(k,u,v) = \underset{w \in S_{k-2}}{\textrm{max}} (\pi(k-1,w,u) \times q(v|w,u) \times e(x_k|v))\)
- Return: \(\textrm{max}_{u \in S_{n-1},v \in S_n} (\pi(n,u,v) \times q(\textrm{STOP}|u,v))\)
We want ‘argmax’, not ‘max’, i.e. the actual most-likely tag sequence.
- Inputs:
- a sentence \(x_1 \ldots x_n\), a sequence of words
- transmisson parameters \(q(s|u,v)\),
- emission parameters \(e(x|s)\).
- Output:
- \(\textrm{arg}\underset{y_1 \ldots y_{n+1}}{\textrm{max}} p(x_1 \ldots x_n, y_1 \ldots y_{n+1})\)
- Initialization:
- Set \(\pi(0,\textrm{*},\textrm{*}) = 1\).
- Definition:
- \(S_{-1} = S_0 = \{\textrm{*}\}\)
- \(S_k = S\;\forall\;k \in \{1 \ldots n\}\)
- Algorithm
- For \(k = 1 \ldots n\):
- For \(u \in S_{k-1}\), \(v \in S_k\):
- \(\pi(k,u,v) = \underset{w \in S_{k-2}}{\textrm{max}} (\pi(k-1,w,u) \times q(v|w,u) \times e(x_k|v))\)
- \(bp(k,u,v) = arg \underset{w \in S_{k-2}}{max} (\pi(k-1,w,u) \times q(v|w,u) \times e(x_k|v))\)
- Set \((y_{n-1},y_n) = \textrm{argmax}_{(u,v)} (\pi(n,u,v) \times q(\textrm{STOP}|u,v))\)
- For \(k = (n-2) \ldots 1\), \(y_k = bp(k+1, y_{k+1}, y_{k+2})\)
- Return the tag sequence \(y_1 \ldots y_n\).
- What is different?
- Don’t just record \(\pi\) at each point but also a backpointer \(bp\); which tag achieved this max. Which tag is most likely at \(k\) given \(u,v\).
- We then have \(\pi\) and \(bp\) values.
- At the end we go backwards in the sequence.
- Run-time complexity is \(O(n \times |S|^3)\).
- We enter the \(u,v\) loop \(n \times |S|^2\) times.
- Each time we enter we need to search over \(|S|\) possible tags.
- It is linear with respect to sentence length.
- Much better than brute force, which was \(O(|S|^n)\).
- HMM taggers are very simple to train.
- Just compile counts from training corpus, calculate MLEs.
- Perform relatively well, over 90% on named entity recognition.
- Main difficulty is modelling: e(word|tag), especially if words are low-frequency.
- One approach is to group low-frequency words into classes, but very clumsy and heuristic.
- When words are complex even worse.
- Later in the course we develop more complex methods.
- Input: a sentence, e.g. “Boeing is located in Seattle”.
- Output: a parse tree.
- leaves of tree: words.
- internal nodes: labels (e.g. S, NP, VP, …)
- Hierarchical decomposition.
- Work in formal syntax goes back to Chomsky’s PhD thesis in 1950s.
- Syntactic Structures, Chomsky, 1957
- More syntactic formalisms:
- Minimalism
- Lexical functional grammar (LFG)
- Head-driven phrase-structure grammar (HPSG)
- Tree adjoining grammars (TAG)
- Categorical grammars.
- But we are going to use context-free grammars (CFGs), which forms the basis of other formalisms.
- We will (again) treat parsing as a supervised learning problem.
- Penn Wall Street Journal Treebank.
- 50k sentences with associated trees, annotated by hands.
- Treebank: set of sentences with associated parse trees.
- “The burglar robbed the apartment”
- First level: part-of-speech tags for each word.
- (N = noun, V = verb, DT = determiner).
- DT -> the
- N -> burglar
- V -> robbed
- DT -> the
- N -> apartment
- Second level: phrases.
- (NP = noun phrases, VP = verb phrases, S = sentences)
- “the/DT burglar/N” is dominated by an internal node “NP”.
- This means the two tagged words are grouped as a noun phrase.
- “robbed the apartment” is a VP.
- “the burglar robbed the apartment” is an S.
- Third level: useful relationships
- subject to verb.
- NP then VP -> V.
- “the/DT burglar/N”/NP is the subject of “robbed”/V, by looking at fragments of the tree.
- verb to direct object.
- VP to V and NP.
- This is verb to direct object.
- “robbed”/V “the/DT apartment/N”/NP.
- English word order: subject -> verb -> object.
Japanese word order: subject -> object -> verb.
- English: IBM bought Lotus
Japanese: IBM Lotus bought.
- English: Sources said that IBM bought Lotus yesterday.
Japanese: Sources yesterday IBM Lotus bought that said.
- The reordering has been applied recursively.
Such reording is difficult to see in a sentence, but consists of rotations in the parse tree (swapping the order).
- Hopcroft and Ullman, 1979
- A CFG \(G = (N, \Sigma, R, S)\), where
- \(N\) is a finite set of non-terminal symbols.
- \(\Sigma\) is a finite set of terminal symbols.
- \(R\) is a finite set of rules of the form \(X \rightarrow Y_1 Y_2 \ldots Y_n\) for \(n \ge 0\), \(X \in N\), \(Y_i \in (N \cup \Sigma)\).
- Each rule’s left hand side must be a non-terminal.
- Each rule’s right hand side may be “empty” ($), a non-terminal, or terminal, or both.
- \(S \in N\) is a distinguished start symbol.
- \(N\) = {S, NP, VP, PP, DT, Vi, Vt, NN, I}
- \(S\) = S
- \(\Sigma\) = {sleeps, saw, man, woman, telescope, the, with in}.
- \(R\):
- S -> NP VP
- VP -> Vi
- VP -> Vt NP
- VP -> VP PP
- NP -> DT NN
- NP -> NP PP
- PP -> IN NP
- Vi -> sleeps
- Vt -> saw
- NN -> man
- NN -> woman
- NN -> telescope
- DT -> the
- IN -> with
- IN -> in
- Symbol meanings:
- S -> sentence
- VP -> verb phrase
- NP -> noun phrase
- PP -> prepositional phrase
- DT -> determiner
- Vi -> intransitive verb
- Vt -> transitive verb
- NN -> noun
- IN -> preposition
- A derivation is a sequence of strings \(s_1 \ldots s_n\) such that:
- \(s_1 = S\); first symbol is the start symbol
- \(s_n \in \Sigma^{*}\), i.e. \(s_n\) is made up of terminal symbols only such that it is the set of all possible strings.
- If \(\Sigma\) = {the, dog, a}, then \(\Sigma^{*}\) = {\(\epsilon\), a, dog, the, a dog, the dog, …}.
- A left-most derivation is such that:
- Each \(s_i\) for \(i = 2, \ldots, n\) is derived from \(s_{i-1}\) by picking the left-most non-terminal \(X\) in \(s_{i-1}\) and replacing it by some \(\beta\) where \(X \rightarrow \beta\) is a rule in \(R\).
- For example, “the man sleeps”.
- [S], [NP VP], [D N VP], [the N VP], [the man VP], [the man Vi], [the man sleeps]
- We “pop as left as possible”.
| S |
S -> NP VP |
| NP VP |
NP -> DT N |
| DT N VP |
DT -> the |
| the N VP |
N -> dog |
| the dog VP |
VP -> VB |
| the dog VB |
VB -> laughs |
| the dog laughs |
|
- Input: “She announced a program to promote safety in trucks and vans”.
- Output:
- Correctly: she’s announcing a program that will promote safety in both trucks and vans.
- Also: she’s announcing a program that will promote safety in trucks, and “vans” (just throwing in the word vans).
- Also: she’s announcing a program that wil promote safety. This program is located within trucks and vans.
- 14 different syntactic structures.
Quiz: given “Jon saw Bill in Paris in June”, and grammar:
- S -> NP VP
- PP -> P NP
- NP -> N
- NP -> NP PP
- VP -> V NP
- VP -> VP PP
- P -> in
- V -> saw
- N -> Jon
- N -> Bill
- N -> June
- N -> Paris
How many parse trees are there for this sentence?
- !!AI I couldn’t get this. First step is probably to draw one valid parse tree. Then, according to the quiz answer:
There are three places to attach the two PPs: the verb, the first noun, the second noun. The five valid derivations are (1) verb, verb, (2) first noun, verb, (3) first noun, second noun, (4) first noun, first noun, (5) verb, second noun.
“A Comprehensive Grammar of the English Language”, 1800 pages, 4.6lbs, 10 inches x 8.4 inches x 2.4 inches :).
- Parts of Speech (tags from the Brown corpus, from the early 1960’s).
- Nouns
- NN = singular noun (e.g. man, dog, park)
- NNS = plural noun (e.g. telescopes, houses, buildings)
- NNP = proper noun (e.g. Smith, Gates, IBM)
- Determiners
- DT = determiner (e.g. the, a, some, every)
- Adjectives
- JJ = adjective (e.g. red, green, large, idealistic)
- NP is a Noun Phrase.
- \(\bar{N} \rightarrow NN\)
- \(\bar{N} \rightarrow NN\enspace\bar{N}\)
- \(\bar{N} \rightarrow JJ\enspace\bar{N}\)
- \(\bar{N} \rightarrow \bar{N}\enspace\bar{N}\)
- \(NP \rightarrow DT\enspace\bar{N}\)
An example
- NN -> box
- NN -> car
- NN -> mechanic
- NN -> pigeon
- DT -> the
- DT -> a
- JJ -> fast
- JJ -> metal
- JJ -> idealistic
JJ -> clay
- NP
- [DT, \(\bar{N}\)]
- [the, \(\bar{N}\)]
- [the, \(NN\)]
[the, car]
and
- NP
- [DT, \(\bar{N}\)]
- [the, \(\bar{N}\)]
- [the, JJ, \(\bar{N}\)]
- [the, fast, \(\bar{N}\)]
- [the, fast, \(NN\)]
- [the, fast, car]
and
- NP
- [DT, \(\bar{N}\)]
- [the, \(\bar{N}\)]
- [the, JJ, \(\bar{N}\)]
- [the, JJ, JJ, \(\bar{N}\)]
- [the, fast, red, car]
- So, intuitively, \(\bar{N} \rightarrow JJ\enspace\bar{N}\) is prepending any number of adjectives to a noun.
- Very similarly, \(\bar{N} \rightarrow NN\enspace\bar{N}\) prepends any number of nouns to a noun (“the car factory”).
- The \(\bar{N}\) category is an intermediate category with these noun phrases. It always follows a determiner.
Quiz: given “the fast car mechanic”, there are three parse trees.
- [ NP [ D the ] [ \(\bar{N}\) [ JJ fast ] [ \(\bar{N}\) [ NN car ] [ \(\bar{N}\) [ NN mechanic ] ] ] ] ]
- “the”, “fast car mechanic”
- [ NP [ D the ] [ \(\bar{N}\) [ \(\bar{N}\) [ JJ fast ] [ \(\bar{N}\) [ NN car ] ] ] [ \(\bar{N}\) [ NN mechanic ] ] ] ]
- “the”, “fast car”, “mechanic”
- [ NP [ D the ] [ \(\bar{N}\) [ JJ fast ] [ \(\bar{N}\) [ \(\bar{N}\) [ NN car ] ] [ \(\bar{N}\) [ NN mechanic ] ] ] ] ]
- “the”, “fast”, “car mechanic”
(draw them out to see).
- Brown corpus uses IN = preposition (e.g. of, in, out, beside, as).
- e.g. “of the man”, “in the room”.
- We add two rules to hand prepositional phrases:
- \(PP \rightarrow IN \enspace NP\)
- \(\bar{N} \rightarrow \bar{N} \enspace PP\)
- Roughly 100 prepositions in English.
- a full triangle in a parse tree means that there are some undefined set of other nodes that make up the words.
- NP, then full triangle, then “the room” as only child.
- \(\bar{N} \rightarrow \bar{N} \enspace PP\) means the prepositional phrase (PP) is a post-modifier to the noun.
- “the dog in the car”; “in the car” is a post-modifier to “dog”.
- !!AI last slide in “An Extended Grammar”, for lecture "A Simple Grammar for English (Part 2) is worth re-watching.
- Basic Verb Types
- Vi = instransitive verb (e.g. sleeps, walks, laughs)
- Vt = transitive verb (e.g. sees, saw, likes)
- Vd = ditransitive verb (e.g. gave)
- Basic VP rules
- \(VP \rightarrow Vi\)
- \(VP \rightarrow Vt \enspace NP\)
- \(VP \rightarrow Vd \enspace NP \enspace NP\)
- Basic S rule
- \(S \rightarrow NP \enspace VP\)
- The NP is the subject.
- The VP generates some verb followed by zero or more noun phrases.
- Examples of VP
- sleeps
- walks
- likes the mechanic
- gave the mechanic the fast car
- Examples of S
- the man sleeps
- the dog walks
- the dog gave the mechanic the fast car
- A new rule: \(VP \rightarrow VP \enspace PP\)
- New examples of VP:
- sleeps in the car
- walks like the mechanic
- gave the mechanic the fast car on Tuesday
- The Prepositional Phrase (PP) usually adds information about the location or the time etc. of the Verb Phrase (VP).
- Complementizers
- COMP = complementizer (e.g. that)
- SBAR
- \(SBAR \rightarrow COMP \enspace S\)
- Examples
- that the man sleeps
- that the mechanic saw the dog
- New Verb Types
- V[5] (e.g. said, reported)
- V[6] (e.g. told, informed)
- V[7] (e.g. bet)
- New VP rules
- \(VP \rightarrow V[5] \enspace SBAR\)
- \(VP \rightarrow V[6] \enspace NP \enspace SBAR\)
- \(VP \rightarrow V[7] \enspace NP \enspace NP \enspace SBAR\)
- Examples of new VPs:
- said that the man sleeps.
- told the dog that the mechanic likes the pigeon.
- the NP is “the dog”
- the SBAR is “that the mechanic likes the pigeon”
- bet the pigeon $50 that the mechanic owns a fast car.
- the V[7] is “bet”. This is a very rare verb category.
- the NP is “the pigeon”
- another NP is “$50”
- the SBAR is “that the mechanic owns a fast car”
- A new part-of-speech
- CC = coordinator (e.g. and, or, but)
- New Rules
- \(NP \rightarrow NP \enspace CC \enspace NP\)
- NP made up of “the man”/NP “and”/CC “the dog”/NP
- \(\bar{N} \rightarrow \bar{N} \enspace CC \enspace \bar{N}\)
- \(VP \rightarrow VP \enspace CC \enspace VP\)
- VP made up of “sleeps”/VP “and”/CC “likes the dog”/VP
- \(S \rightarrow S \enspace CC \enspace S\)
- \(SBAR \rightarrow SBAR \enspace CC \enspace SBAR\)
- Agreement
- “The dogs laugh” vs. “The dog laughs”
- Some notion of agreement between verb and main subject. Our current grammar fails to capture this constraint.
- Wh-movement
- “The dog that the cat liked …”
- “cat” is a transitive verb (Vt). Really “dog” should come after it, but it’s moved to the start.
- Active vs. passive
- The dog saw the cat vs.
- The cat was seen by the dog
- For more information: Syntactic Theory: A Formal Introduction, 2nd edition. Ivan A. Sag, Thomas Wasow, and Emily M. Bender.
- Second source: prepositional phrase attachment.
- “I drove down the road in the car”.
- “I” “drove down the road” “in the car”
- “I” “drown down” “the road in the car”
- “John was believed to have been shot by Bill”
- Bill shot John.
- Bill believed that John has been shot.
- Despite both interpretations being, a prior, equally likely, humans have a strong tendency to attach prepositional phrases to the most recent verb. Hence 1) is more intuitive.
- Third source: noun premodifiers
- “the fast car mechanic”
- “the” “fast” “car mechanic”
- “the” “fast car” “mechanic”
- Probability assigned to each rule.
- Hence probability assigned to each possible parse tree when ambiguity presence.
- Naive application is very poor, but simple to make better.
- Every rule, even the rules that lead only to terminal symbols (e.g. \(Vi \rightarrow \textrm{sleeps}\)), has a probability associated with it.
- Probability of a tree \(t\) with rules:
\[\alpha_1 \rightarrow \beta_1, \alpha_2 \rightarrow \beta_2, \ldots, \alpha_n \rightarrow \beta_n\]
- \(p(t) = \prod_{i=1}^{n} q(\alpha_i \rightarrow \beta_i)\), where \(q(\alpha \rightarrow \beta)\) is the probability for rule \(\alpha \rightarrow \beta\).
- Note that the sum of all probabilities for a particular \(\alpha_i\) left-hand-side (LHS) non-terminal is 1.
- Top-down stochastic processe where we can sample parse trees.
| S |
S \(\rightarrow\) NP VP |
1.0 |
| NP VP |
NP \(\rightarrow\) DT NN |
0.3 |
| DT NN VP |
DT \(\rightarrow\) the |
1.0 |
| the NN VP |
NN \(\rightarrow\) dog |
0.1 |
| the dog VP |
VP \(\rightarrow\) Vi |
0.4 |
| the dog Vi |
Vi \(\rightarrow\) laughs |
0.5 |
| the dog laughs |
|
|
- The process ends when we have no non-terminals left.
Quiz: consider the following PCFG:
- q(S -> NP VP) = 0.9
- q(S -> NP) = 0.1
- q(NP -> D N) = 1
- q(VP -> V) = 1
- q(D -> the) = 0.8
- q(D -> a) = 0.2
- q(N -> cat) = 0.5
- q(N -> dog) = 0.5
- q(V -> sings) = 1
And parse tree:
(S, (NP, (D, the), (N, cat)), (VP, (V, sings)))
Probability:
| S |
S -> NP VP |
0.9 |
| NP VP |
NP -> D N |
1 |
| D N VP |
D -> the |
0.8 |
| the N VP |
N -> cat |
0.5 |
| the cat VP |
VP -> V |
1 |
| the cat V |
V -> sings |
1 |
| the cat sings |
|
|
Total probability = \(0.9 \times 1 \times 0.8 \times 0.5 \times 0.5 \times 1 \times 1 = 0.36\)
- Assigns a probability to each left-most derivation, or parse-tree, allowed by the underlying CFG.
- Assume:
- sentence \(s\),
- set of derivations for that sentence \(T(s)\)
- Thus PCFG assigns probability \(p(t)\) to each derivation in \(T(s)\).
- There is a ranking in order of probability.
- The most likely parse tree for sentence \(s\) is \(\textrm{arg} \underset{t \in T(s)}{\textrm{max}} p(t)\)
Quiz: consider the following PCFG:
- q(S -> NP VP) = 1.0
- q(VP -> VP PP) = 0.9
- q(VP -> V NP) = 0.1
- q(NP -> NP PP) = 0.5
- q(NP -> N) = 0.5
- q(PP -> P NP) = 1.0
- q(N -> Ted) = 0.2
- q(N -> Jill) = 0.2
- q(N -> town) = 0.6
- q(V -> saw) = 1.0
- q(P -> in) = 1.0
Given sentence “Ted saw Jill in Town”, what is highest probability for any parse tree under this PCFG?
Right now there’s no clever way, just brute force. Also note that just because a PCFG parse tree has a non-zero probability doesn’t mean it’s a valid left-most derivation.
I could only find two valid left-most derivations; intuitively they are:
- Ted “saw” “Jill in town”, i.e. Jill was in town when Ted saw her.
- Ted “saw Jill” “in town”, i.e. Ted was in town and saw Jill.
Strictly speaking the parse trees and corresponding probabilities are:
(S, (NP, N, Ted), (VP, (V, saw), (NP, (NP, N, Jill), (PP, (P, in), (NP, N, town))))), = 0.00015
(S, (NP, N, Ted), (VP, (VP, (V, saw), (NP, N, Jill)), (PP, (P, in), (NP, in town)))) = 0.00027
Note that these probabilities do not add up to 1; not all possible PCFG parse-trees are valid left-most derivations.
- Penn WSJ Treebank = 50,000 sentences with associated trees
- Usual set up: 40,000 training sentences (80%), 2,400 test sentences (4.8%).
- Given a set of examples (a treebank), the underlying CFG can simply be all the rules seen in the corpus.
- Maximum Likelihood estimates:
\[q_{ML}(\alpha \rightarrow \beta) = \frac{\textrm{Count}(\alpha \rightarrow \beta)}{\textrm{Count}(\alpha)}\]
\[q_{ML}(\textrm{VP} \rightarrow \textrm{Vt NP}) = \frac{\textrm{Count}(\textrm{VP} \rightarrow \textrm{Vt NP})}{\textrm{Count}(\textrm{VP})}\]
- where the counts are taken from a training set of example trees.
- If the training data is generated by a PCFG, then as training data size goes to infinite, the maximum-likelihood PCFG will converge to the same distribution as the “true” PCFG.
Quiz: given these three parse trees, what’s \(q_{ML}(\textrm{NP} \rightarrow \textrm{NP PP})\)? It’s 2/7.
- Booth and Thompson (1973) show that a CFG with rule probabilities correctly defines a distribution over the set of derivations provided that:
- The rule probabilities define conditional distributions over the different ways of rewriting each non-terminal.
- A technical condition on the rule probabilities ensuring that the probability of the derivation terminating in a finite number of steps is 1. (This condition is not really a practical concern).
- Consider “S -> S S” with probability 1.0, “S -> a” with probability 0.
- But more interesting is that “S -> S S” with probability 0.6, “S -> a” with probability 0.4 also fails. Not elaborated on.
- Given a PCFG and a sentence \(s\), define \(T(s)\) to be the set of trees with \(s\) as the yield.
- Given a PCFG and a sentence \(s\), how do we find:
\[\textrm{arg} \underset{t \in T(s)}{\textrm{max}} p(t)\]
- We could enumerate, brute force.
- Find all trees.
- Calculate probabilities for each tree.
- Find tree with maximum probability.
- This is exponential, but can be efficiently solved using dynamic programming.
- Assume CFG \(G = (N, \Sigma, R, S)\) is in Chomsky Normal Form, as follows:
- \(N\) is a set of non-terminal symbols.
- \(\Sigma\) is a set of terminal symbols.
- \(R\) is a set of rules which take one of two forms:
- \(X \rightarrow Y_1 Y_2\) for \(X \in N\), and \(Y_1, Y_2 \in N\)
- \(X, Y_1, Y_2\) are all non-terminals
- \(X \rightarrow Y\) for \(X \in N\), and \(Y \in \Sigma\).
- \(X\) is non-terminal, \(Y\) is terminal.
- \(S \in N\) is a distinguished start symbol.
- You can take any PCFG and convert it to a PCFG in Chomsky Normal Form.
- “VP -> Vt NP PP”, with probability 0.2
- Introduce a new symbol.
- “VP -> Vt-NP PP”, with probability 0.2
- “Vt-NP -> Vt NP”, with probability 1.0
- This just introduces intermediary non-terminals; to move from Chomsky Normal Form back to the original PCFG just remove these dummy non-terminals.
- Notice that the original rule with three non-terminals has the same probability as the new rule with two non-terminals; this is also the answer to the quiz.
- Given a PCFG and a sentence \(s\), how do we find:
\[\underset{t \in T(s)}{\textrm{max}} p(t)\]
- (we really want argmax, but we’ll do that later).
- Notation:
- \(n\) = number of words in the sentence
- \(w_i\) = \(i\)’th word in the sentence
- \(N\) = the set of non-terminals in the grammar
- \(S\) = the start symbol in the grammar
- Define a dynamic programming table
- \(\pi[i,j,X]\) = maximum probability of a constituent with non-terminal \(X\) spanning words \(i \ldots j\) inclusive
- \(i = 1, 2, \ldots, n\)
- \(j = 1, 2, \ldots, n\)
- \(X \in N\)
- Our goal is to calculate \(max_{i \in T(S)} p(t) = \pi[1,n,S]\).
- “What is the proability of the most likely parse tree that has S at the root and spans all the words in the sentence?”
- Assume sentence \(w_1, w_2, w_3, w_4, w_5, w_6\).
- \(\pi(2, 5, NP)\) means "what is the probability of the most likely way of having an NP in the parse tree such that it dominates / spans \(w_2, w_3, w_4, w_5\) inclusive?
\[\underset{1}{\textrm{the}} \enspace \underset{2}{\textrm{dog}} \enspace \underset{3}{\textrm{saw}} \enspace \underset{4}{\textrm{the}} \enspace \underset{5}{\textrm{man}} \enspace \underset{6}{\textrm{with}} \enspace \underset{7}{\textrm{the}} \enspace \underset{8}{\textrm{telescope}}\]
\(\pi(3, 8, \textrm{VP})\) is all VPs that span words 3 to 8 inclusive.
- the dog using the telescope to see the man
- the dog seeing a man with the telescope
- The \(\pi\) statement is “which of the two is the more likely spanning VP?”
- Base case definition: \(\forall i = 1, 2, \ldots, n, \forall X \in V\):
\[\pi[i,i,X] = q(X \rightarrow w_i)\]
- Note: define \(q(X \rightarrow w_i) = 0\) if \(X \rightarrow w_i\) is not in the grammar.
e.g. “the/1 dog/2 laughs/3”, \(\pi(2,2,\textrm{NN})\) only has one possible parse tree because it must be “NN -> dog”, hence \(= q(\textrm{NN} \rightarrow \textrm{dog})\)
Recursive definition: \(\forall i = 1, 2, \ldots, (n-1)\), \(j = (i+1), \ldots, n\), \(X \in N\):
\[\pi(i,j,X) = \underset{\underset{s \in i \ldots (j-1)}{X \rightarrow Y \enspace Z \in R}}{max} (q(X \rightarrow Y \enspace Z) \times \pi(i,s,Y) \times \pi(s+1,j,Z))\]
- \(s\) is the split point.
\[\underset{1}{\textrm{the}} \enspace \underset{2}{\textrm{dog}} \enspace \underset{3}{\textrm{saw}} \enspace \underset{4}{\textrm{the}} \enspace \underset{5}{\textrm{man}} \enspace \underset{6}{\textrm{with}} \enspace \underset{7}{\textrm{the}} \enspace \underset{8}{\textrm{telescope}}\]
\(\pi(3,8,\textrm{VP})\)
Suppose we have:
- VP -> Vt NP, probability 0.4
- VP -> VP PP, probability 0.6
We’re searching over two possible things:
- We’re searching over all possible rules in the grammar (\(X \rightarrow Y \enspace Z \in R\)).
- We’re searching over all possible split points (\(s \in i \ldots (j-1)\)).
- \(s \in \{3, 4, 5, 6, 7\}\).
\[
\begin{align}
&\begin{aligned}
& q(\textrm{VP} \rightarrow \textrm{VT NP}) \times \pi(3,3,\textrm{Vt}) \times \pi(4,8,NP) \\
& q(\textrm{VP} \rightarrow \textrm{VT NP}) \times \pi(3,4,\textrm{Vt}) \times \pi(5,8,NP) \\
& \vdots \\
& q(\textrm{VP} \rightarrow \textrm{VT NP}) \times \pi(3,7,\textrm{Vt}) \times \pi(8,8,NP) \\
& q(\textrm{VP} \rightarrow \textrm{VT PP}) \times \pi(3,3,\textrm{Vt}) \times \pi(4,8,PP) \\
& q(\textrm{VP} \rightarrow \textrm{VT PP}) \times \pi(3,4,\textrm{Vt}) \times \pi(5,8,PP) \\
& \vdots \\
& q(\textrm{VP} \rightarrow \textrm{VT PP}) \times \pi(3,7,\textrm{Vt}) \times \pi(8,8,PP)
\end{aligned}
\end{align}
\]
- Each of these products will have a different value, and the max is the value for \(\pi(3,8,\textrm{VP})\).
- We will calculate the \(pi\) values bottom-up to ensure correctness.
- Consider the above example yet again.
- Suppose for \(\pi(3,8,\textrm{VP})\) we choose “VP -> VP PP”.
- And suppose we also choose split point \(s = 5\).
- This means that the first right-hand-side \(VP\) spans \(w_3, w_4, w_5\), and the second right-hand-side \(PP\) spans \(w_6, w_7, w_8\).
- The highest probability tree is formed of two child trees, which themselves must be the highest probabilities trees, etc.
- This is a classic observation of “dividing a problem into equivalent subproblems”, i.e. dynamic programming.
Input: a sentence \(s = x_1 \ldots x_n\), a PCFG in Chomsky Normal Form (CNF) \(G = (N, \Sigma, S, R, q)\).
Initialization:
\(\forall \enspace i \in \{1, \ldots, n\}, \forall \enspace X \in N,\)
\[
\begin{equation}
\pi(i,i,X) = \begin{cases}
q(X \rightarrow x_i), & \textrm{if} \enspace X \rightarrow x_i \in R \\
0, & \textrm{Otherwise}
\end{cases}
\end{equation}
\]
Algorithm
- For \(l = 1 \ldots (n-1)\)
- For \(i = 1 \ldots (n-l)\)
- Set \(j = i + l\)
- \(\pi(i,j,X) = \underset{\underset{s \in i \ldots (j-1)}{X \rightarrow Y \enspace Z \in R}}{max} (q(X \rightarrow Y \enspace Z) \times \pi(i,s,Y) \times \pi(s+1,j,Z))\)
- and
- \(bp(i,j,X) = \textrm{arg}\underset{\underset{s \in i \ldots (j-1)}{X \rightarrow Y \enspace Z \in R}}{max} (q(X \rightarrow Y \enspace Z) \times \pi(i,s,Y) \times \pi(s+1,j,Z))\)
- \(l\) is the length of the segment we’re filling in.
- Hence we go from smallest to largest, satisfying the rule that we do small lengths first.
- l = 1
- i = 1, j = 2
- i = 2, j = 3
- i = 3, j = 4
- l = 2
- i = 1, j = 3
- i = 2, j = 4
- The runtime is \(O(n^3 \times |N|^3)\)
- Cubic with respect to number of words \(n\).
- Also cubic with respect to the number of non-terminals in the grammar, \(|N|\).
- Consider that there are \(n^2\) choices for \((i,j)\).
- There are \(|N|\) choices for X, then \(\times |N|^2\) when considering \(Y\) and \(Z\).
- And \(s\) also varies with \(n\).
- This is way easier than brute-force search.
- PCFGs augments CFGs by including a probability for each rule in the grammar.
- The probability for a parse tree is the product of probabilities for the rules in the tree.
- To build a PCFG-parsed parser:
- Learn a PCFG from a treebank.
- Given a test data sentence, use the CKY algorithm to computer the highest probability tree for the sentence under the PCFG.
- Note that every rule to a terminal is independent of every other part of the parse tree; very strong and wrong independence assumption.
- Attachment ambiguity Attachment decision for prepositional phrases (PP) is completely independent of the words.
- We know this is a bad decision.
- Coordination ambiguity: for the coordinator (CC), could be e.g.
- “dogs in houses” “and” “cats”, or
- “dogs” “in” “houses and cats”
- e.g. “president of a company in Africa”
- “president” “of a” “company in Africa”, or
- “president” “of a company” “in Africa” (president in Africa)
- Both parse have the same rules, therefore receive the same probability under a PCFG.
- Close attachment (“Africa” attaching to “company” because it’s close) is twice as likely in WSJ test.
- Previous example: “John was believed to have been shot by Bill”
- Here the low attachment analysis (Bill does the shooting) contains the same rules as the high attachment analysis (Bill does the believing), so the two analyses receive same probability.
- Vi -> sleeps
- Vt -> saw
- NN -> man
- NN -> woman
- NN -> telescope
- DT -> the
- IN -> with
- IN -> in
- For each rule that give non-terminals, identify one of the children to be the head of the rule. An additional piece of information.
- Each context-free rule has one “special” child that is the head of the rule, the most special part, the syntactic centre, e.g.
- S -> NP VP, (VP is the head)
- VP -> Vt NP, (Vt is the head)
- NP -> DT NN NN (NN is the head)
- A core idea in syntax
- See X-bar Theory, Head-Driven Phrase Structure Grammar
- Some intuitions:
- The central sub-constituent of each rule.
- The semantic predicate in each rule.
- Many early treebanks, e.g. WSJ, do not contain annotations for the heads.
- If the rule contains NN, NNS, or NNP:
- Choose the rightmost NN, NNS, or NNP.
- Else If the rule contains an NP:
- Else If the rule contains a JJ
- Else If the rule contains a CD (number, e.g. “100”, “1000”)
- Else
- Choose the right-most child
e.g.
NP -> DT NNP NN NP -> DT NN NNP* NP -> NP PP NP -> DT JJ NP -> DT
- If the rule contains Vi or Vt (or indeed all subcategories of verbs):
- Choose the leftmost Vi or Vt
- Else If the rule contains a VP
- Else
- Choose the leftmost child
e.g.
VP -> Vt NP VP -> VP PP
- We’re going to add lexical information to each non-terminal to our tree.
- Rather than one single “S”, we could have e.g. “S(questioned)”
- Whereas we had around 50 non-terminals before, now we could have \(50 \times |V|\), where \(V\) is vocabulary size, so in the thousands.
- We will propogate heads up the tree.
- A constituent receives its headword from its head child.
- S -> NP VP, (S receives headword from VP)
- VP -> Vt NP, (VP receives headword from Vt)
- NP -> DT NN, (NP receives headword from NN).
- For rules that go to a terminal (e.g. DT -> the), the contituent receives the word as its headword (e.g. DT becomes DT(the)).
- (see earlier slide about CNF)
- (recall the complexity of CYK algorithm is \(O(n^3 \times |N|^3)\), where \(n\) is length of string being parsed, \(N\) is number of non-terminals).
- \(N\) is a set of non-terminal symbols
- \(\Sigma\) is a set of terminal symbols
- \(R\) is a set of rules which take one of three forms:
- \(X(h) \rightarrow_1 Y_1(h) Y_2(w)\) for \(X \in N\), and \(Y_1, Y_2 \in N\), and \(h, w \in \Sigma\).
- e.g. VP(saw) \(\rightarrow_1\) Vt(saw) NP(dog)
- X = VP
- \(Y_1\) = Vt
- \(Y_2\) = NP
- h = saw
- w = dog
- The subscript on the arrow indicates where the head word comes from, the first \(Y\).
- \(X(h) \rightarrow_2 Y_1(w) Y_2(h)\) for \(X \in N\) and \(Y_1, Y_2 \in N\) and \(h, w \in \Sigma\).
- e.g. S(saw) \(\rightarrow_2\) NP(man) VP(saw).
- \(X(h) \in h\) for \(X \in N\) and \(h \in \Sigma\).
- e.g. DT(the) -> the, where X = DT and h = the.
- \(S \in N\) is a distinguished start symbol.
- The subscript on the arrows are important because it disambiguates e.g.
- NP(dog) -> NN(dog) NN(dog).
S(saw) \(\rightarrow_2\) NP(man) VP(saw)
NP(saw) \(\rightarrow_1\) Vt(saw) NP(dog)
NP(man) \(\rightarrow_2\) DT(the) NN(man)
NP(dog) \(\rightarrow_2\) DT(the) NN(dog)
Vt(saw) \(\rightarrow\) saw
DT(the) \(\rightarrow\) the
NN(man) \(\rightarrow\) man
NN(dog) \(\rightarrow\) dog
- When drawing parse tree put a big dot on the branch that indicate where the head word is coming from.
- An example parameter in a regular PCFG
\[q(\textrm{S} \rightarrow \textrm{NP VP})\]
- An example parameter in a Lexicalized PCFG
\[q(\textrm{S(saw)} \rightarrow_2 \textrm{NP(man) VP(saw)})\]
- Technically a Lexicalized PCFG is just a regular PCFG with many, many more non-terminals.
- However, qualitatively what’s happened is that we have much less data per terminal.
- This is a similar problem to language modelling with more n-grams, and will have a similar solution.
- The new form of grammar looks just like a Chomsky normal form CFG, but with potentially \(O(|\Sigma|^2 \times |N|^3)\) possible rules.
- Naively, parsing an \(n\) word sentence using the dynamic programming algorithm will take \(O(n^3 |\Sigma|^2 |N|^3)\) time.
- But \(|\Sigma|\) can be huge!!
- Crucial observation: at most \(O(n^2 \times |N|^3)\) rules can be applicable to a given sentence \(w_1, w_2, \ldots, w_n\), of length n. This is because any rules which contain a lexical item that is not one of \(w_1 \ldots w_n\) an be safely discarded.
- e.g. given “the dog saw the cat”
- If rule is “S(questioned) ->2 NP(dog) VP(questioned)”, it can be discarded because “questioned” not in sentence.
- The result: we can parse in \(O(n^5 |N|^3)\) time.
- \(n^3\) comes from dynamic programming algorithm.
- \(n^2\) comes from the idea we need to use words from the sentence.
- \(|N|^3\) comes from CNF usage of non-terminals.
- An example parameter in a Lexicalized PCFG:
\[q(\textrm{S(saw)} \rightarrow_2 \textrm{NP(man) VP(saw)})\]
- First step: decompose this parameter into a product of two parameters
\[
\begin{align}
&\begin{aligned}
& q(\textrm{S(saw)} \rightarrow_2 \textrm{NP(man) VP(saw)}) \\
= & q(\textrm{S} \rightarrow_2 \textrm{NP VP|S, saw}) \times q(\textrm{man|S} \rightarrow_2 \textrm{NP VP, saw})
\end{aligned}
\end{align}
\]
- First parameter: given that I have S(saw) what is the probability of re-writing it as “NP VP”?
- Second parameter: say we have S(saw) and we know we have NP on the left and VP(saw) on the right.
- What will fill in the NP(???)
- What is the probability that “man” is chosen for the NP?
- Second step: use smoothed estimation for the two parameter estimates
\[
\begin{align}
&\begin{aligned}
& q(\textrm{S} \rightarrow_2 \textrm{NP VP | S, saw}) \\
= & \lambda_1 \times q_{ML}(\textrm{S} \rightarrow_2 \textrm{NP VP | S, saw}) + \lambda_2 \times q_{ML} (S \rightarrow_2 \textrm{NP VP | S}) \\ \\
& q(\textrm{man | S} \rightarrow_2 \textrm{NP VP, saw}) \\
= & \lambda_3 \times q_{ML} (\textrm{man | S} \rightarrow_2 \textrm{NP VP, saw}) + \lambda_4 \times q_{ML}(\textrm{man | S} \rightarrow_2 \textrm{NP VP}) + \lambda_5 \times q_{ML} (\textrm{man | NP})
\end{aligned}
\end{align}
\]
- The first parameter:
- The second parameter:
- Very similar reasoning.
- \(\lambda_3, \lambda_4, \lambda_5 \ge 0\), \(\lambda_3 + \lambda_4 + \lambda_5 = 1\).
- \(\lambda_3\) asks “given S(saw), NP(???), and VP(saw), what is the probability of the NP having man?”
- Throw away “saw”, \(\lambda_4\) asks “given S(h), NP(???) and VP(h), where h is some head word, what’s the probability of the NP having man?”
- \(\lambda_4\) asks “given NP(???) what’s the probability of the NP having man?”
- Again, robustness vs. sensitivity, bias vs. variance.
- Need to deal with rules with more than two children, e.g.
- VP(told) -> V(told) NP(him) PP(on) SBAR(that)
- One way is to binarize using method covered before, adding intermediate non-terminals.
- Need to incorporate parts of speech (useful in smoothing)
- VP-V(told) -> V(told) NP-PRP(him) PP-IN(on) SBAR-COMP(that)
- Need to encode preferences for close attachment.
- “John was believed to have been shot by Bill”.
- Won’t be covered in this course. Further reading:
- Michael Collins, 2003. “Head-Driven Statistical Models for Natural Language Parsing”. In Computational Linguistics.
- Take some parse tree.
- Break up into constituents with labels, start points, end points.
- “the/1 lawyer/2 questioned/3 the/4 witness/5”
| NP |
1 |
2 |
| NP |
4 |
5 |
| VP |
3 |
5 |
| S |
1 |
5 |
- We do not include parts of speech in this defintion. What’s missing is “the/DT lawyer/NN questioned/Vt the/DT witness/NN”.
- Take the output from human parsed data, this is our gold standard.
- Take output parsed using our PCFG.
- Create two sets of tables for the constituents.
- \(G\) = number of constituents in gold standard = 7.
- \(P\) = number of constituents in parse output = 6.
- $C = number correct = 6.
- How many rules in the parse output are also in the gold standard?
- Recall = \(\textrm{100%} \times \frac{C}{G} = \textrm{100%} \times \frac{6}{7}\)
- Precision = \(\textrm{100%} \times \frac{C}{P} = \textrm{100%} \times {6}{6}\).
- Training data: 40k sentences from the Penn Wall Street Journal treebank. Testing: around 2.4k sentences from the Penn Wall Street Journal treebank.
- Results for a PCFG: 70.6% Recall, 74.8% Precision.
- Magerman (1994): 84.0% Recall, 84.3% Precision.
- Based on Decision trees and bottom-up parser.
- Results for a lexicalized PCFG: 88.1% recall, 88.3% precision (from Collins (1997, 2003)
- More recent results:
- 90.7%/91.4% (Carreras et al 2008)
- Discriminative estimation
- 91.7%/92.0% (Petrov 2010)
- 91.2%/91.8% (Charniak and Johnson, 2005)
- Discriminative estimation
- Recall two of the three rules of lexicalised PCFGs:
- \(X(h) \rightarrow_1 Y_1(h) Y_2(w)\)
- \(X(h) \rightarrow_2 Y_1(w) Y_2(h)\)
- see slides for lexicalised PCFG parse tree of “the man saw the dog with the telescope”
- Dependencies (format: (h, w, rule))
- (ROOT_0, saw_3, ROOT)
- (saw_3, man_2, S ->2 NP VP)
- (man_2, the_1, NP ->2 DT NN)
- (saw_3, with_6, VP ->1 VP PP)
- (saw_3, dog_5, VP ->1 Vt NP)
- (dog_5, the_4, NP ->2 DT NN)
- (with_6, telescope_8, PP ->1 IN NP)
- (telescope_8, the_7, NP ->2 DT NN)
- Always same number of dependencies as number of words, in this case 8.
- Special dependency for the start symbol.
(Numbers taken from Collins (2003))
- Subject-verb pairs (S \(\rightarrow_2\) NP VP): over 95%/95% recall/precision.
- Object-verb pairs (VP \(\rightarrow_1\) Vt NP$) (“saw the man”): over 92%/92% recall/precision.
- Other arguments to verbs (VP 1 Y1 Y_2$): 92%
- Non-recursive NP boundaries: 93%
- PP attachments (\(X(h) \rightarrow Y_1(h) PP(w)\)): 82%
- Coordination ambiguities: 61%.
- Takeaway
- Core structure is good.
- Modifiers cause difficulties.
- This is from 1997, but would see same breakdown of per-type dependency accuracies in modern parsers.
- Key weakness of PCFGs: lack of sensitivity to lexical information
- Lexicalised PCFGs:
- Lexicalize a treebank using head rules.
- Estimate the parameters of a lexicalized PCFG using smoothed estimaton.
- Accuracy of lexicalized PCFGs: around 88% in recovering constituents or dependencies.
- All parses for a sentence with \(n\) words have \(n\) dependencies. Report a single figure, dependency accuracy.
- Results from Collins 2003: 88.3% dependency accuracy.
- Can calculate precision/recall on particular dependency types,
- e.g. look at all subject/verb dependencies \(\implies\) all dependencies with label \(\textrm{S} \rightarrow_2 \textrm{NP VP}\).
- Recall = \(\frac{\textrm{number of subject/verb dependencies correct}}{\textrm{number of subject/verb dependencies in gold standard}}\)
- Precision = \(\frac{\textrm{number of subject/verb dependencies correct}}{\textrm{number of subject/verb dependencies in parser's output}}\)
- p96: a word is the full inflected or derived form of a word.
- In English n-gram models are based on wordforms, not the lemmas, i.e. root.
- e.g. cat is the lemma, cats is the inflected wordform.
- p96: n-gram models, and counting words in general, requires tokenization or text normalization; separating out punctuation, dealing with abbreviations, normalizing spelling, etc.
- p96: a type is a distinct word in a corpus.
- p96: a token is any instance of a word in the corpus.
- p102: typically divide our data ito 80% training, 10% development, and 10% test.
- p104: quadrigram sentences based on Shakespeare are actually real Shakespeare.
- The n-gram probability matrices are very sparse.
- p104: be sure to choose similar training and test copurses. Don’t choose from different genres.
- p105: closed vocabulary assumes we know all the words in the vocabulary.
- This can’t possibly be exactly true.
- There will be out of vocabulary (OOV) words.
- The percentive of OOV words in the test set is called the OOV rate.
- An open vocabulary is one where we model OOV words by adding a pseudo-word called
<UNK>. We train these probabilities as follows:
- Choose a fixed vocabulary in advance.
- Convert in the training set any OOV word to the unknown word token
<UNK> in a text normalization step.
- Estimate the probabilities for
<UNK> from its counts just like any other regular word in the training set.
- p105: extrinsic evaluation of language models is best; apply them to your problem and see which is best.
- difficult in practice, so use intrinsic evaluation instead, which measures quality independent of any application.
- perplexity is the most common intrinsic evaluation metric.
- Perplexity is a weighted average branching factor of a language. The number of possible next words that can follow any word.
- p107: It is closely related to the information theoretic notion of entropy.
- p108: smoothing is modifications made to address poor estimates that are due to variability in small data sets.
- pull in probabiliy mass from higher counts, pile it on to zero counts.
- p108: Laplacian smoothing.
p111: Good-Turing Discounting
- Use count of things you’ve seen once (singletons or hapax legomenons) to re-estimate the frequency of zero-count things.
- The frequency of frequency c is the number of n-grams that occur c times.
- More formally:
\[N_c = \sum_{x\;:\;\textrm{Count(x)} = c} 1\]
- The MLE count for \(N_c\) is \(c\). The Good-Turing estimate replaces this with a smoothed count \(c^*\), as a function of \(N_{c+1}\):
\[c^* = (c+1)\frac{N_{c+1}}{N_c}\]
- We can use the equation above to replace the MLE counts for all the bins \(N_1, N_2, \ldots\).
- However, instead of using this equation directly to re-estimate the smoothed count \(c^*\) for \(N_0\), use the following which we can call the missing mass:
\[P_{GT}^{*}\;\textrm{(things with frequency zero in training)} = \frac{N_1}{N}\]
- Here \(N_1\) is the count of items in bin 1, i.e. seen once in the training set, and \(N\) is the total number of items we have seen in training.
- p113: some advanced issues in Good-Turing estimation
- p114: Good-Turing discounting is not used by itself; it’s only used in combination with backoff and interpolation, discused later.
- p118: practical issues: toolkits and data formats
- Since probabilities by definition are less than 1, the more probabilities we multiply together tha smaller they become.
- Hence we use log probabilities rather than raw probabilities, and add in log space rather than multiply in linear space.
- In order to report probabilities just take the “exp” of the logprob:
\[p_1 \times p_2 \times p_3 \times p_4 = exp(log p_1 + log p_2 + log p_3 + log p_4)\]
- Backoff N-gram language models are generally stored in ARPA format
- Small header.
- List of all non-zero N-gram probabilities (all unigrams, followed by bigrams, followed by trigrams, etc).
- Each N-gram entry is stored with its discounted log probabiliy (in \(\textrm{log}_{10}\) format) and its backoff weight \(\alpha\).
- Backoff weights only necessary if the N-gram forms a prefix of a longer N-gram.
- Thus, for trigram grammar, the format of each N-gram is:
p119: e.g.
\data\
ngram 1=1000
ngram 2=10000
ngram 3=5000
\1-grams:
-0.4405 </s>
-99 <s>
-4.34443 the -1.43973
-4.5325 dog -4.3438
<snip>
\2-grams:
-3.43535 <s> i -5.353535
-4.43333 i went 0.0430843
...
\3-grams:
-3.3245 <s> i prefer 3.434
...
- In training mode each toolkit takes a raw text file, one sentence per line, words separated by white-space.
- It also takes parameters such as order \(N\), thresholds, type of discounting.
It outputs a language model in ARPA format.
In perplexity or decoding mode the toolkit take a language model in ARPA format, a sentence or corpus, and produces the probability and perplexity of the sentence or corpus.
- p119: Advanced smoothing methods: Kneser-Ney Smoothing
- p121: it turns out that any interpolation model can be represented as a backoff model, hence stored in ARPA backoff format.
- p121: class-based N-grams.
- p122: language model adaptation and using the web
- use web search hits to estimate trigram language model parameters.
works well in practice, even though only getting page counts and not word counts back.
- p122: using longer distance information: a brief summary
- state of the art systems use 4-grams and 5-grams.
- After 6-grams up to 20-grams, Goodman found that no useful improvement.
- cache model: use the preceding part of a test corpus and mix it into your trained language model when making predictions.
- words are often repeated.
- only works well in domains where you have perfect knowledge of words.
- topic-based: train different language models for different kinds of words.
- latent-semantic indexing: measure probability based on the word’s similarity to preceding words, mix it in.
- trigger: a word that is not adjacent but highly related, so we mix it in.
- skip N-grams: we skip over an intermediate word.
variable-length N-grams: adjust context size.
pruning by removing low-probability events is important, and essential on low-power platforms like cellphones.
Example:
\data\
ngram 1=19979
ngram 2=4987955
ngram 3=6136155
\1-grams:
-1.6682 A -2.2371
-5.5975 A'S -0.2818
-2.8755 A. -1.1409
-4.3297 A.'S -0.5886
-5.1432 A.S -0.4862
...
\2-grams:
-3.4627 A BABY -0.2884
-4.8091 A BABY'S -0.1659
-5.4763 A BACH -0.4722
-3.6622 A BACK -0.8814
...
\3-grams:
-4.3813 !SENT_START A CAMBRIDGE
-4.4782 !SENT_START A CAMEL
-4.0196 !SENT_START A CAMERA
-4.9004 !SENT_START A CAMP
-3.4319 !SENT_START A CAMPAIGN
...
\end\